機械学習エンジニアのための将棋AI開発入門その2

前回の続き。将棋AIで最初に大規模機械学習に成功させたBonanzaの開発者である保木さんのインタビューがちょうどYahoo!ニュースのトップ記事として掲載されたところなので、今回はBonanzaの機械学習について数学的な観点から解説してみたいと思います。

Bonanzaの保木さんのインタビュー記事

プロ棋士に迫ったAI「Bonanza」　保木邦仁「将棋を知らないから作れた」
https://news.yahoo.co.jp/feature/1712

BonanzaのGPW発表スライド

とは言え、Bonanzaで使われている機械学習の技法は、いまどきの機械学習とは少し毛色が異なるので心の準備が必要です。

まず、保木さんのGPW(ゲームプログラミングワークショップ)での発表スライド、以前はBonanzaの公式サイトからダウンロードできたのですが、Bonanzaの公式サイトがジオシティーズにあったため、ジオシティーズのサービス終了に伴い、見れなくなってしまいました。現在では、情報処理学会(IPSJ)のサイトから閲覧できるようです。

ゲーム木探索の最適制御：将棋における局面評価の機械学習
https://www.ipsj.or.jp/10jigyo/forum/software-j2008/hoki-print.pdf

上記の資料のことを、以下では「BonanzaのPDF」と書きます。

Bonanzaの更新式

まず、目的関数Jを設定(設計)します。プロの棋譜を教師として、その教師棋譜の指し手が指せると目的関数Jの値が小さくなるように設定します。(後述します)

評価関数は、前回やったKPP型なので、評価関数パラメーターのベクトルを$w$、入力(出現している3駒関係の特徴)ベクトルを$x$として、ベクトルの内積、もしくは次のように行列表現で書けます。

$$Eval(\textbf{x}) = \textbf{w}^T\textbf{x}$$

それではまずBonanzaの更新式を見ていきましょう。

BonanzaのPDF、10ページ目が、更新式です。このスライドでは、Jが目的関数、評価関数パラメーターは、$\nu$(ギリシア文字の「ニュー」)で表されています。(適宜、読み替えてください)

$h$は学習率で、SGDなどの更新式の$\eta$(eta、ギリシア文字の「イータ」)に相当するものです。

$\displaystyle{\frac{\partial J}{\partial \nu}}$の部分は勾配です。目的関数を評価関数パラメーター(のベクトル$\nu$)で偏微分したものです。以下、単に「勾配」と書いた場合、これを指すものとします。

つまり、評価関数パラメーターのベクトルを$\nu$ではなく$w$と書くとして、上式は次のように書き直せます。

$$w ← w\space-\space \eta \cdot sign(\displaystyle{\frac{\partial J}{\partial w}})$$

そう見ると、SGDの更新式に非常によく似ています。この式はsignさえなければ、SGDの更新式そのものです。機械学習の教科書によく載っているやつですね。

オンライン機械学習 (機械学習プロフェッショナルシリーズ)

created by Rinker

上式に出てくるsignとは次のような符号を返す関数です。

$$sign(x) = \begin{cases} +1 & (x>0) \\ 0 & (x=0) \\ -1 & (x<0) \end{cases}$$

実際はさきほどのBonanzaの更新式では、sign()にはベクトルを引数にとっています。この時、ベクトルの各要素に対して、sign()を適用するものとします。(PythonのNumPyで言うところのbroadcastingです)

SGDの更新式だと、勾配に比例した分だけ動かすのですが、それは動かしすぎだと保木さんはおっしゃるわけですね。目的関数Jが凸凹(でこぼこ)なのでそんな無理はできないだろうと。

実際のところ、Bonanza以降の将棋ソフトの大規模機械学習では、SGDやAdamでの学習に成功させ、それがそのあとのブレイクスルーにも繋がっていくのですが、上式とは目的関数の設計自体が異なるので、Bonanzaの目的関数において、SGDやAdamで学習が成功するのかどうかは私にはわかりません。

将棋ソフトなのはの開発者のかずさんから、2014年ごろ、Bonanzaの学習部の改造において、慣性項(加速度？)をつけてもうまく学習できたという発言があった気がします。つまり、毎回、-1,+1ずつ評価関数パラメーターの各要素の値を動かすのではなく、前回と同じ方向にその要素の値を動かすときには、-2,+2、そのまた次回にも同じ方向に動かすならば、-4,+4のように倍々にしていくことで早くに値を学習させることはできたとのこと。その程度の改良はできるようです。

いずれにせよ、Bonanzaでは、目的関数Jの勾配と逆方向に評価関数パラメーターを -1 , +1 するのを繰り返すだけという大変シンプルな作りになっています。

Bonanzaの目的関数

次に、Bonanzaの目的関数について見ていきます。BonanzaのPDF 7ページ目。

ここで後者の式に出てくるTはシグモイド関数です。前回の記事では、KPP型の評価関数を学習させるときに、シグモイド関数を通して評価値を勝率に変換したあと、cross entropyを使ってゴニョゴニョしました。

教師局面と学習させたい局面との評価値の差ですと、終盤になるほど発散してしまい(終盤ほど勝ち(+∞)/負け(-∞)に向かって評価値が発散していくので)、差をそのまま目的関数に組み込むと、序盤が重視されず、序盤の学習がほとんどなされません。

そこで、評価値の差ではなく、-1から1の間ぐらいの数値で、教師局面と学習させたい局面の評価値が似ているかを判定できる関数が欲しいわけです。前回のように勝率に変換しても良いのですが、上式では、2つの評価値の差に対してシグモイド関数を適用することで、その2つの評価値が近いかどうかを判定して(数値化して)います。

また、シグモイド関数の性質により、絶対値が大きい値に対してはその勾配は0に近くなります。2つの評価値がかけ離れているとき、差の絶対値が大きくなるので、シグモイド関数の勾配は0に近くなります。このため、あまりに評価値がかけ離れた局面は学習には使用されません。

上のようにTにシグモイド関数を用いる場合、終盤で、例えば教師の評価値が1000で、学習させたい局面の評価値が1100の局面があったとして、形勢としてはこの２つは微差なので、序盤の評価値の100点の差ほどには重視して欲しくないのですが、これらが同様の扱いになるので、終盤に対して特化した(終盤を重視するような)学習になりがちです。

なので、現代の視点で見ると、この部分は、あまりよろしくない設計であると私は思います。

「Bonanzaは攻撃的な棋風」と当時言われたのも、逆に言うと序盤が粗く、悪い仕掛けをしてしまい、だけど終盤力で勝つという勝ち方を数多くしたからではないかと私は考えています。

あと、上のスライド、いくつかわかりにくいところがあるので初学者のために補足しておきます。

目的関数がJ’となっていますが、これは目的関数を微分したものではなく、ここでは普通に目的関数です。このページのあと、目的関数をここから修正していくので、最終的な目的関数がJで、その修正前のものがJ’と思ってください。
局面Pは、(プロの)棋譜に出現した局面です。プロの棋譜は2004年当時、4万局程度使用されていたと思いますが、この棋譜に出現した局面をPとします。
Mは合法手の数ですが、そのなかに棋譜の指し手も含まれています。ただし、mが棋譜の指し手である場合は、T[ ] の中身が 0 になるので考えなくてすみます。
後者の式の∑は、m=1からMと局面Pの合法手すべてに対して計算してありますが、こうしてしまうと合法手が多い局面ほど∑が大きな値となってしまうのでよくありません。実際は、Bonanzaでは棋譜の指し手に近い評価値を持つ指し手数手に対してのみ∑の中身を計算しています。αβ探索なので、探索の結果得られる評価値が、ある値から外れるかどうかはわりと小さな探索コストで求めることができます。なので、棋譜の指し手で進めた評価値に近い評価値を持つ指し手を求めるのはそれほど大きな探索コストではありません。
$p_m$は「局面Pを合法手mで進めた子局面」とありますが、正確には「(直接の)子局面」ではなく、mで1手進めたあと探索(Bonanzaではdepth 3で探索)したときの末端の局面(PV leaf : 最善応手列の末端)です。
棋譜の指し手より高い評価値をつける指し手(の3手先)の局面の評価値が、棋譜の指し手を指したときの評価値より下がって欲しいので、学習対象の局面は、この棋譜の指し手ではない指し手で1手進めたあとdepth 3で探索させたときのPV leafの局面です。その局面で出現しているKPPの特徴因子に対して、求めた勾配により、さきほどの更新式を使って評価関数パラメーターを調整します。
評価関数パラメーターが更新されるのは、batch学習なのですべての棋譜のすべての局面に対する勾配(を足し合わせたもの)が求まってからです。このため評価関数パラメーターを1回更新するのにすごく時間がかかります。また1回の更新で-1,0,+1しかしないのでわずかしか値が動きません。あと、各局面でdepth 3で探索しているのでその探索コストが馬鹿になりません。Bonanzaでは、最初depth 2で学習させて、仕上げとしてdepth 3で学習させるというような手法で学習させたらしいです。それでも当時のPC(Xeon)で学習に数ヶ月要したそうです。
学習時に探索を伴い、その探索は評価関数パラメーターの内容を依存するので、更新式により評価関数パラメーターが更新されていくと探索の結果(PV leafや探索の評価値)が変化します。このため、batchで繰り返し更新式を適用すると言っても同じ教師データを与えて続けているのとはちょっと事情が異なります。評価関数パラメーターを更新していくと、探索の質が改善され、教師の質が上がってくるので、強化学習的な側面もあると言えます。

補足だけでわりと息切れしてきましたので、次いきましょう…。

正則化項

KPPの評価関数の特徴ベクトルの次元(評価因子の数)が、2億次元あるという話を前回の記事でしました。プロ棋士の棋譜が4万棋譜、平均手数が140手として、560万局面しかなく、未知数が2億個、式が560万個からなる連立方程式が解けますか？という話になります。

方程式の数が全然足りていないことは明らかで、このままでは過学習(over-fitting)してしまいます。このことを簡単に説明するためにPRML(『パターン認識と機械学習』)のFigure 1.4を引用します。

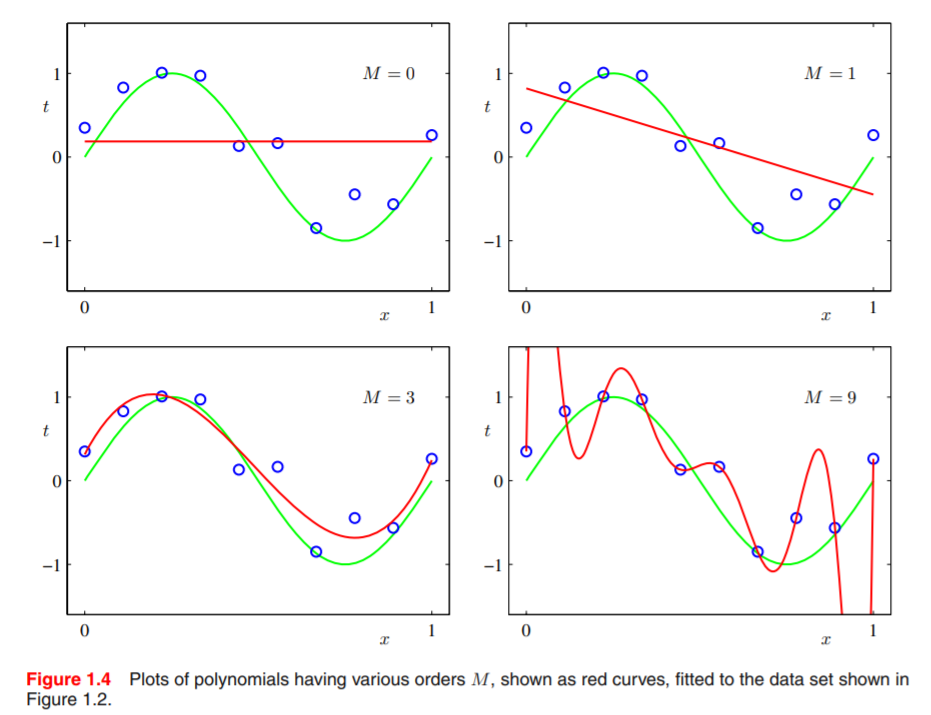
上図は、9個の標本点(青いプロット)が与えられた時にそれを多項式近似しようとしていて、Mがその多項式の次数です。上図の右下の例では、M=9なので9次方程式で近似しようとしています。右下の例の赤い曲線は、何も考えずに最小二乗法で9次方程式の係数を求めてみた場合です。9次方程式なので9個の狙った点を通ることはできるのですが、いびつな形の曲線になっており、このあとやってくるであろう標本点の良い近似になっているとは言えないでしょう。すなわち、汎化性能が低いような近似と言えます。

これを回避するために、多項式の各係数があまり大きな値にならないように次のような制約のもとで最小化問題を解くことを考えます。

L1正則化 : $ J = |w_1| + |w_2| + \cdots + |w_n| → min $

L2正則化 : $ J = |w_1|^2 + |w_2|^2 + \cdots + |w_n|^2 → min $

前者は各成分を1乗、後者は各成分を2乗してあるので、この正則化項はそれぞれL1ノルム、L2ノルムと呼ばれます。(より正確には後者はL2ノルムの2乗ですが)

L1,L2ノルムについては次の記事を参考にしていただくとします。

ノルムの意味とL1，L2，L∞ノルム
https://mathtrain.jp/lpnorm

また、正則化にL1ノルムを使う場合はラッソ回帰(Lasso regression)、L2ノルムを使う場合、リッジ回帰(Ridge regression)と呼ばれることがあります。詳しくはググってください。

さきほどのJ’と同様に、このような正則化項も同時に最小化したいので、ラグランジュの未定乗数法を使います。

$$ 新しい目的関数J = さきほどのJ’ + \lambda_2 \cdot M_2(\nu) $$

$M_2$は、$\nu$の大きさを求める関数です。例えば、L2正則化だとすると、$M_2(\nu) = \nu_1^2 + \nu_2^2 + \cdots = \nu^{T}\nu$です。BonanzaのPDFだと「ベクトルの大きさ」としか書かれていませんが、そのソースコードからは、L1正則化だと思います。

また、$\lambda_1$(このあと出てくる) , $\lambda_2$は、ラグランジュの未定定数とします。

あと、Bonanzaでは、駒割(駒自体の点数)をある程度高めに固定したかったようです。駒の盤面上の位置評価よりは駒割(一番たくさん出現する特徴)にまずそれなりの点数がついて欲しいというのは、わからないではありません。

そこで、$M_1$は、$\nu$のうち、駒割に関する成分だけの大きさを求める関数として、駒割ベクトルの大きさ$M_1(\nu) = M_0$($M_0$は定数)の条件下で、さきほどのJ’を最小化したいと考え、ここでもラグランジュの未定乗数法を使います。

$M_1(\nu) – M_0 = 0$と右辺が0になる形に変形して式をひとまとめにすると

$$ 新しい目的関数J = さきほどのJ’ + \lambda_1[M_1(\nu) – M_0] + \lambda_2 \cdot M_2(\nu)$$

のようになります。

この式に相当するのがBonanzaのPDFの9ページ目です。変数名は少し違うので適宜読み替えてください。

ようやく、目的関数が導出できましたので、あとは目的関数Jを評価関数パラメーター$\nu$で偏微分します。

Tはシグモイド関数です。その微分は前回記事でやりました。
∑の[ ]の中身は、さきほどやった、(学習対象局面の探索の評価値 – 教師局面の探索の評価値 ) です。
$\nabla_{\nu}M_1(\nu)$は、BonanzaのPDFには「駒割りに関する特徴ベクトル要素の大きさ等」とあるので、この項は、駒割に関するL1ノルムの微分だと思うのですが、ソースコード上には出てきてないと思うので、よくわかりません。歩の価値を100点に正規化するようなコード自体は書かれていたと思うのですが…。
$\nabla_{\nu}M_2(\nu)$は、L1ノルムの微分です。L1ノルムには絶対値がついているので、本来は微分できませんが、ここでは、そのベクトルの各成分 xは、 x > 0 のときはその微分は +1 , x < 0のときその微分は -1として扱います。(つまりは、sign(x) ) 詳しくは劣微分などでググってみてください。

ここで、さきほどの更新式を再掲します。

$$w ← w\space-\space \eta \cdot sign(\displaystyle{\frac{\partial J}{\partial w}})$$

Jの勾配の(各成分の)符号と逆方向に評価関数パラメーターを更新しています。正則化項の偏微分は、(L1正則化の場合、上の補足 4. にあるように) sign(x) として扱うので、上の更新式では、評価関数パラメーターを更新するときに、その成分をちょっぴり0方向に引っ張ってやることになります。

例えば、batchを通じて、一度も出現しなかった特徴に関しては、その勾配(の成分)は0になりますが、上の正則化項があるため、勾配はsign(x)となり、その結果、更新式によりwのその成分は0に引張られていきます。この結果、出現回数が少ないだとか、勾配の絶対値が小さいだとかするような成分はすべて 0 になります。

あまり出現しないということは勾配情報自体の信憑性に乏しいということなので、勾配成分の符号を信じてsign()で-1,+1ずつ同じ方向に動かし続けるなどして変に発散されたりするよりは0になってくれたほうがマシという意味もあります。

そんなわけで、Bonanzaでは、このようなL1正則化項をつけることで評価関数パラメーターが発散するのを防いでいました。

Bonanza 6.0のソースコードから

参考のため、Bonanza 6のソースコードから更新式のまわりの処理を引用します。日本語コメントは私が記入しました。上までの説明と少し違う箇所がありますが、まあ、スライドの発表当時から、改良されたのかなと…。

// pvは評価関数パラメーターのある成分のポインタ
// dvはそれに対応する勾配(スカラー値) , ただし符号は反転している。
static void
rparam( short *pv, float dv )
{
  int v, istep;

  // brand()は0か1の乱数を返す関数。binary randの意味か？
  // ここでは、それを2回足すことでベルヌーイ試行を
  // 2回やった確率分布にして、二項分布(正規分布風)の乱数にしている。
  istep  = brand();
  istep += brand();

  // vは、評価関数パラメーターのある成分
  v      = *pv;

  // vの符号に応じて0に引っ張るための処理。L1正則化に相当。
  if      ( v > 0 ) { dv -= (float)FV_PENALTY; }
  else if ( v &lt; 0 ) { dv += (float)FV_PENALTY; }

  // 勾配の符号に応じて、+1,-1する。
  // (実際は+1,-1ではなく、istep(乱数)を足している。)
  // dvの符号は反転しているので、dvが正ならvを+1、負ならvを-1する。
  // 各パラメータが同時に全く同じように動くと鞍点にtrapされかねないので
  if      ( dv >= 0.0 &amp;&amp; v &lt;= SHRT_MAX - istep ) { v += istep; }
  else if ( dv &lt;= 0.0 &amp;&amp; v >= SHRT_MIN + istep ) { v -= istep; }
  else { out_warning( "A fvcoef parameter is out of bounce.\n" ); }

  *pv = (short)v;
}

// pvは評価関数パラメーターのある成分のポインタ

// dvはそれに対応する勾配(スカラー値) , ただし符号は反転している。

static void

rparam( short *pv, float dv )

{

int v, istep;

// brand()は0か1の乱数を返す関数。binary randの意味か？

// ここでは、それを2回足すことでベルヌーイ試行を

// 2回やった確率分布にして、二項分布(正規分布風)の乱数にしている。

istep = brand();

istep += brand();

// vは、評価関数パラメーターのある成分

v = *pv;

// vの符号に応じて0に引っ張るための処理。L1正則化に相当。

if ( v > 0 ) { dv -= (float)FV_PENALTY; }

else if ( v < 0 ) { dv += (float)FV_PENALTY; }

// 勾配の符号に応じて、+1,-1する。

// (実際は+1,-1ではなく、istep(乱数)を足している。)

// dvの符号は反転しているので、dvが正ならvを+1、負ならvを-1する。

// 各パラメータが同時に全く同じように動くと鞍点にtrapされかねないので

if ( dv >= 0.0 && v <= SHRT_MAX - istep ) { v += istep; }

else if ( dv <= 0.0 && v >= SHRT_MIN + istep ) { v -= istep; }

else { out_warning( "A fvcoef parameter is out of bounce.\n" ); }

*pv = (short)v;

}

評価関数の大規模機械学習に向けて

Bonanzaのあとに出てくるような将棋AIの評価関数の大規模機械学習では、教師の局面を大量に生成してそれを学習に用いるようになります。(いわゆる強化学習)

100億局面程度は生成するのが普通という状況になっていきます。大量に標本点が得られる場合、正則化項はむしろ邪魔でしかありません。

例えば、さきほどの多項式近似にしても、9個の標本点しか得られないために過学習しただけで、これがその次数の10倍程度の標本が得られるのならば、過学習はほとんどしません。以下にPRMLのFigure 1.6を示します。この右図が標本点N = 100のケースです。

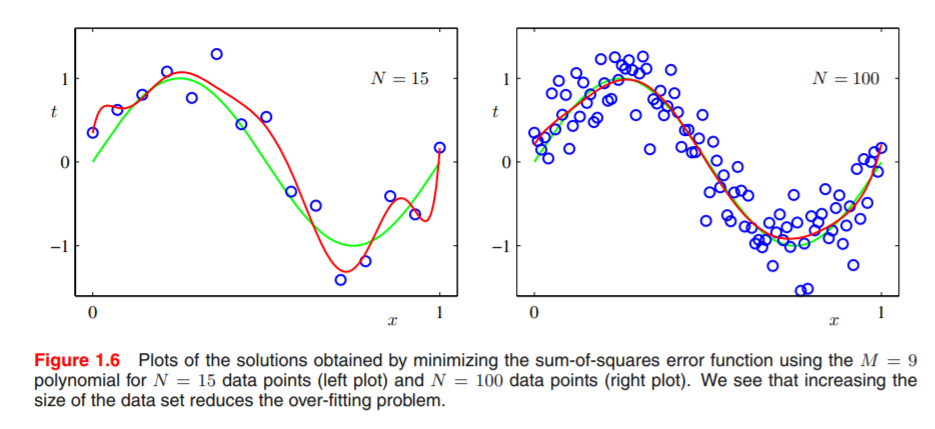
このケースは、適切にfitting(曲線に当てはめ)できているように見えます。一般的に、標本点が増えてくると正則化項がなくとも汎化性能が高いモデルが得られます。

そこで、Bonanza以降の将棋AIの2017年ぐらいまでの流れとしては、評価関数パラメーターを限りなく増やして(評価関数自体の表現力自体を極限まで高めて)、そのパラメーター数の10倍以上の教師を用意して正則化項をつけずに学習させるというパワープレイが横行し始めます。

具体的に言うと、KPPに手番をつけたKPPT(特徴ベクトル、4億次元)だとか、玉2枚と残り2枚の4駒関係KKPPT(特徴ベクトル、300億次元)だとか…。そのために教師局面を100億から、多い時は1000億以上用意するのが普通(?)になっていきます。

このへんの話は次回記事で書けたら書きます。

まとめ

Bonanzaにおける機械学習は、いまどきよくあるような機械学習フレームワーク任せの機械学習ではなく、目的関数の設計に始まっていて、それを(機械学習フレームワークの自動微分に頼るのではなく)自分の手で目的関数を偏微分し、更新式自体も自分で用意して…と非常に手作り感があり、いまの機械学習エンジニアの人たちが見ても新鮮に目に映るのではないでしょうか。

Bonanzaの開発者の保木さんは光化学の研究者をされていたそうで、その分野の専門家ではない私は資料を読み解くだけで一苦労しました。何か本記事に間違いがあれば、コメント欄で教えていただければ幸いです。

おまけ1 PRML

現在、PRML(英語版)は無料でダウンロードできます。

https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf

この日本語版のほうは、この手の技術書としては珍しく、かなりいい翻訳になっていて、英語の得意な人でも日本版を買って、英語版と読み比べると英語の勉強になったりします。😅

パターン認識と機械学習上

created by Rinker

Amazon

あとは、PRMLのアンチョコ(副読本)として、herumiさんの書かれた同人誌、こちらもPDF版が無料ダウンロードできます。併せて読むと理解が進むと思います。

『パターン認識と機械学習の学習普及版』
https://herumi.github.io/prml/

おまけ2 歴史的資料

あと、Bonanzaの最初にWCSC(世界コンピュータ将棋選手権)に出場した前後の歴史的資料として、東大将棋、将棋クエストなどの開発者である、棚瀬寧さんがcafeいっぷく店主の藤田麻衣子さんのYouTubeのチャンネルに最近出演されて語っておられたので、その動画をおまけとして貼り付けておきます。