【連載】評価関数を作ってみよう！その11

前回の続き。今回は、利きの方角ごとの価値について考えます。

将棋は前からの攻めと横からの攻め、どちらが受けにくい？

いま先手の王様が88にいるとします。この時、後手の飛車が前方(82とか)から王手されるのと、横(28とか)から王手されるのとどちらが受けにくいでしょうか？

まあ、状況によるとは思いますが、前からの攻めは、87歩のように歩で止まります。ところが横からの攻めが歩で止まるとは限りません。将棋の初心者の方からは、「78に歩を打てばいいじゃん」という声が聞こえてきそうですが、77に歩があると78歩は二歩なわけです。

そもそも初期陣形では、先手は7段目に歩が並んでいるわけで、8段目に歩を打つためには、この7段目の歩を突いていって、相手に同歩と取られるか、成るか、何らかしなければいけません。先手は、8段目の味方の利きがあるところの筋の歩がこのように切れていて、そこに歩が打てるとは限らないわけです。

さらに前からの攻めとして、△85香と足された場合について考えてみましょう。この場合、先手は79桂と受けて87に利かせることができます。

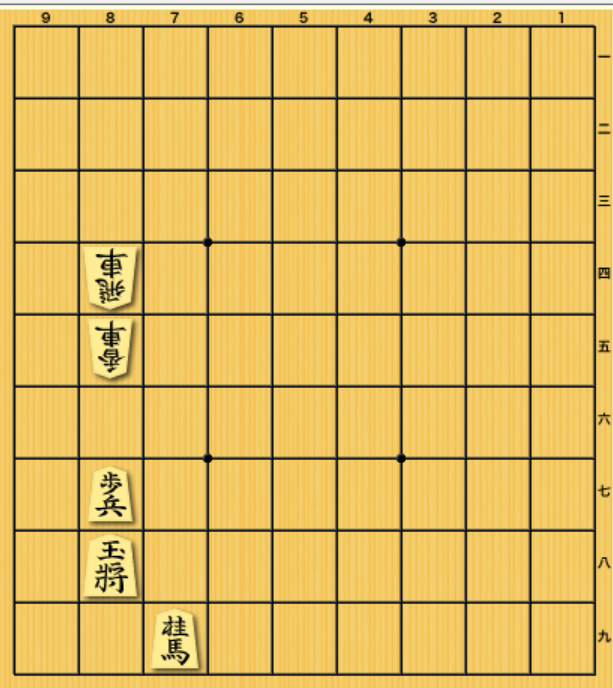
ところがこれが横からの攻め(△28飛とか)だと、▲78合に対して△66桂のように足された場合、先手は78に桂を打って利かせることができません。先手が桂で利きを足すことができるのは7段目から前の段です。(1～7段目)　8,9段目には桂を利かせることができないのです。

このように、先手の王様が8段目にいることを想定すると前からの攻めは歩や桂で受かる分だけ横からの攻めより受けやすのです。

これは上に書いたように
・初期陣形で歩が7段目に並んでいる
・同じ筋に歩が二枚打てない(二歩)
・飛車のように横に遠方まで利く駒がある
・桂のように1～7段目にしか利かない駒がある
から起こりうることであって、初期陣形で歩が切れていたり、飛車のように横に遠方まで利く駒が存在しないのであれば、話は違ってきます。

だから、将棋の初期陣形がどうなっているのかだとか駒の特性の話を抜きにして「横からのほうが受けにくい」とは言えないわけです。

この連載では、利きの価値を出発点として、なるべくどんなサイズの盤面、どんな初期陣形、どんな駒の特性であってもそこそこうまく機能するように考えてきました。

しかし、通常の将棋に限って言えば、このように横からの攻めのほうが受けにくいのは事実ですので、「利きの(王様から見た)方角ごとにその価値が異なる」というのは当然の帰結であるように思われます。

方角ごとに利きの価値を調整する

まず方角を分類します。王様から見て「前」と「後ろ」でもいいですし、「右上」「左上」「左下」「右下」でもいいでしょう。また王様の升によっても利きの威力は異なるでしょう。58に王様がいるときに右上から攻められるのと、99に王様がいるときに右上から攻められるのとでは響きかたが違うからです。(前者は左に逃げられる分だけ、右上からの攻めの価値が低いと考えられる)

しかしまあ、升×方角のすべての組み合わせの利きの価値を求めるとなるとわりとパラメーターが多くなります。そういうのは機械学習するときにやればいいことで、いまは、ざっくりと知りたいだけですので、王様の升ごとの調整はしないものとします。また方角は、次図のように分類します。

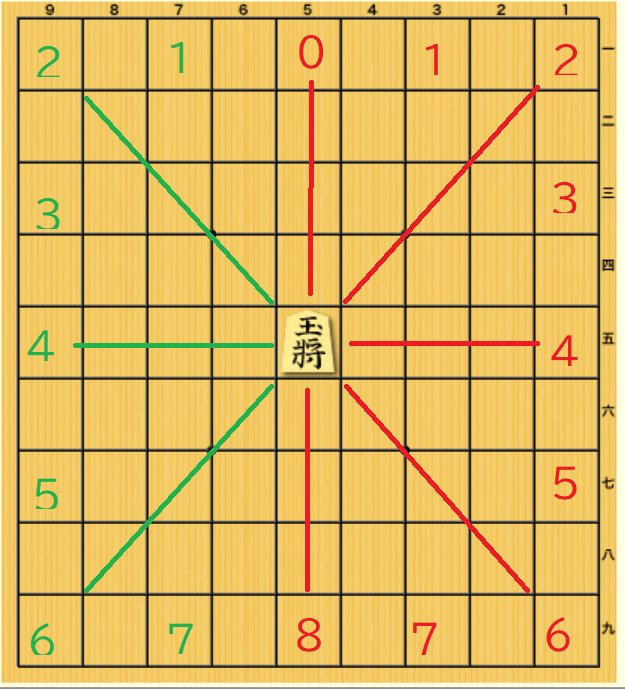
真上は0、右斜め45度上(右上)は2、その間の升(右上上)は1、のように割当たっているものとします。左右は反転させて同じ番号を振るものとします。(右が4で、左も4)

わりと方角を細かく分類したのは、上図の5と6、7でそれぞれ価値がどれくらい異なるか見たかったからです。そんなに変わらないなら前方と後方だけに分類する程度でいいでしょうし。

方角を判定するコード

方角を判定するコードはこうなります。なるべくバグらないように愚直に書きました。

// 先手玉にとってsqの升はどっちの方角であるかを返す。
// 返し値
//   0 :  真上
//   1 :  右上上
//   2 :  右上
//   3 :  右右上
//   4 :  右
//   5 :  右右下
//   6 :  右下
//   7 :  右下下
//   8 :  真下
//   9 :  同じ升
// 左半分に関しては、ミラーして扱い、上記と同じ値となる。
//
int direction_of(Square king, Square sq)
{
    // 筋の差、段の差
    int df = int(file_of(sq) - file_of(king));
    int dr = int(rank_of(sq) - rank_of(king));

    // sqが玉から見て左側にいればsqを(玉から見て)ミラーする。
    // すなわち、筋の差が正なら、符号を反転させる。
    if (df > 0) df = -df;

    // バグらせないように愚直に書く。
    if (df ==  0 &amp;&amp; dr == 0) return 9;

    if (df ==  0 &amp;&amp; dr &lt; 0 ) return 0;
    if (df >  dr &amp;&amp; dr &lt; 0 ) return 1;
    if (df == dr &amp;&amp; dr &lt; 0 ) return 2;
    if (df &lt;  dr &amp;&amp; dr &lt; 0 ) return 3;
    if (df &lt;   0 &amp;&amp; dr == 0) return 4;
    if (df &lt; -dr &amp;&amp; dr > 0 ) return 5;
    if (df ==-dr &amp;&amp; dr > 0 ) return 6;
    if (df ==  0 &amp;&amp; dr > 0 ) return 8; // こっち先にしないと7に含まれてしまう
    if (df > -dr &amp;&amp; dr > 0 ) return 7;

    // ここには、こないはず。
    ASSERT(false);
    return -1;
}

// 先手玉にとってsqの升はどっちの方角であるかを返す。

// 返し値

// 0 : 真上

// 1 : 右上上

// 2 : 右上

// 3 : 右右上

// 4 : 右

// 5 : 右右下

// 6 : 右下

// 7 : 右下下

// 8 : 真下

// 9 : 同じ升

// 左半分に関しては、ミラーして扱い、上記と同じ値となる。

int direction_of(Square king, Square sq)

{

// 筋の差、段の差

int df = int(file_of(sq) - file_of(king));

int dr = int(rank_of(sq) - rank_of(king));

// sqが玉から見て左側にいればsqを(玉から見て)ミラーする。

// すなわち、筋の差が正なら、符号を反転させる。

if (df > 0) df = -df;

// バグらせないように愚直に書く。

if (df == 0 && dr == 0) return 9;

if (df == 0 && dr < 0 ) return 0;

if (df > dr && dr < 0 ) return 1;

if (df == dr && dr < 0 ) return 2;

if (df < dr && dr < 0 ) return 3;

if (df < 0 && dr == 0) return 4;

if (df < -dr && dr > 0 ) return 5;

if (df ==-dr && dr > 0 ) return 6;

if (df == 0 && dr > 0 ) return 8; // こっち先にしないと7に含まれてしまう

if (df > -dr && dr > 0 ) return 7;

// ここには、こないはず。

ASSERT(false);

return -1;

}

方角ごとの利きの価値は？

optimizerに尋ねてみました。

まず方角ごとの味方の利きの価値から。次の配列は、さきほどの図の方角の番号(0が上、1が右上上、2が右上、…)の順番にその価値が並んでいます。

// 方角ごとの利きの価値
// ※　direction_of(king_sq,sq)で返ってきた値ごとに。
// このテーブルの値 / 1024 を利きの価値に掛ける。

int our_effect_rate&#91;10]   = { 1120, 1872,  112,  760, 744, 880, 1320, 600,  904 , 1024 };

// 方角ごとの利きの価値

// ※　direction_of(king_sq,sq)で返ってきた値ごとに。

// このテーブルの値 / 1024 を利きの価値に掛ける。

int our_effect_rate[10] = { 1120, 1872, 112, 760, 744, 880, 1320, 600, 904 , 1024 };

味方の利きで一番価値が高いのは右上上(左上上)方向、1872です。通常の利きの価値を1024と考えているので、通常の利きの価値より、1872/1024 ≒ 1.8倍ぐらいの価値があるとのことのようです。

真上は1120で、1024よりは大きいので少し価値は高いですが、1872ほどではありませんね。まあさきほど書いたように真正面からの単純な攻めは歩で受かりますから、真上を守っても仕方ない意味がありますし。

味方の利きで２つ目に大きな価値があるのは、下方向の1320です。1320/1024 ≒ 1.29倍の価値があるようです。まあ、王様の真下に利きがないと何かの時に尻金で詰みそうです。

続いて、敵の利きの価値はこうなりました。

int their_effect_rate&#91;10] = { 1056, 1714, 1688, 1208, 248, 240,  496, 816,  928 , 1024 };

1	int their_effect_rate[10] = { 1056, 1714, 1688, 1208, 248, 240, 496, 816, 928 , 1024 };

敵の利きの価値で一番高いのは、1714(王様から見て右上上,左上上)、二番目は1688(右上,左上)です。意外にも真上が1056なので、あまり高くありませんね。まあ、さきほど出てきたように歩で受かるからという意味はあるのかも。

それより、真横が248とすこぶる低いです。これは、真横の利きというと敵の飛車を想像しがちですけど、実際には、と金なども含まれるわけで、そう考えると価値が低いのはなんとなく頷けます。

また、右右下が240と最低のスコアをつけました。これは、おそらく、ここに利きをつけている駒(下図のように「と」などであると考えられる)を王様に近づけようとするときに二手かけてやっと左上に1升移動できるのに対して(緑色の矢印)、先手の王様は一手で左上の升に移動できるので、追いかける時の効率が倍も違うことになるためだと思われます。

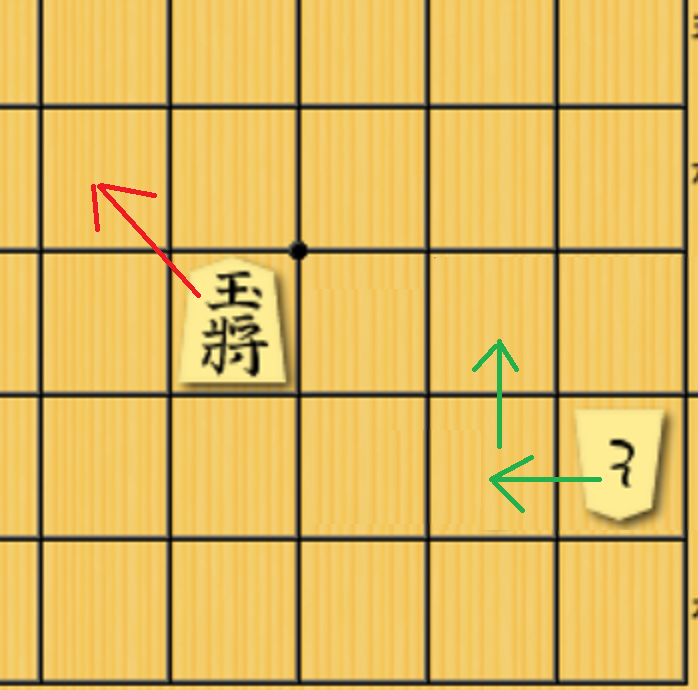
このように、右右下の利きには、そこに利きをつけている駒のpositionalな価値が合算されて計算されて、それゆえ低い値がついているのかも知れません。我々は、利きだけを考えているつもりが、このように細かく利きの種類を分類してしまうと、駒のpositionalな価値を暗黙のうちに含めてしまっています。

この改良でどれだけ強くなる？

前のバージョンから、短い時間(2スレ1手1秒)で+R30、長い時間(2スレ1手4秒)では+R50以上の差があるようでした。もっと長い時間をかけると差はさらに開きそうです。

簡単な改良でわりと強くなって驚いているのですが、利きの方角ごとの価値には、positionalな価値が暗黙のうちに含まれており、それが棋力に大きな差を生み出す要因になっているのだと思われます。

挟撃ボーナス

59に先手玉がいるとして、その右隣の升(49)に相手の駒の利きが2つあるのと、48と68に1つずつ相手の駒の利きがあるのとどちらが嫌ですか？というと、当然後者でしょう。

このような挟撃形をいかにモデル化してうまく表現できるかが一つの課題だと思いますし、逃げにくさ(王様に対する安全度)が適切に表現できるモデルを考えていかなければなりません。

しかし、いま作っている評価関数は、一つ一つの升に順番に着目して、その価値を足し合わせているだけですので、挟撃形が評価できていません。

将棋ソフト『技巧』の評価関数も本連載とわりと似た形をしているので、そういう意味では技巧の評価関数も挟撃形があると評価を誤りやすいと言えそうです。

三駒関係では挟撃形を認識はできますが、しかし、そこにボーナスが何らか加算されているとして、二重に挟撃になっている時にボーナスが加算されすぎるという問題があります。

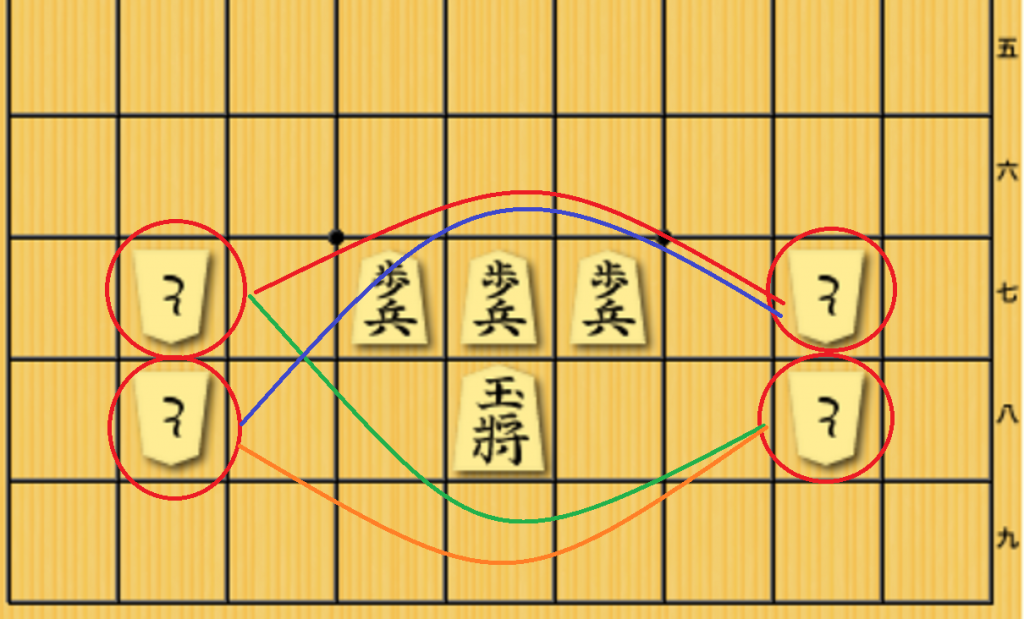
上図では、二重に挟撃になっているため、三駒関係では、挟撃ボーナスが4回加算されていると考えられます。本来の4倍も加算されてしまうと、攻めている側がすごく有利だと評価してしまうことになります。(実際は、先手の王様は▲56歩と突いて上部に逃げられそうなのに)

このように挟撃形を適切に評価すれば強くなるはずではあるものの、三駒関係では挟撃を高く評価しすぎる傾向にあります。

挟撃形については、本連載ではこれ以上は扱いません。各自、考えてみてください。

次回予告

次回、最終回「さよならは言わないで」です。お楽しみに！(予告とは、異なる内容の場合がございます。予めご了承願います。)