WCSC31(第31回 世界コンピュータ将棋選手権)でQugiyは、飛び利き(飛車や角、香のように遠方まで利く駒の利きのこと)に関して、新しいテクニックを披露しました。そのQugiyのアルゴリズムをやねうら王に取り込む予定だったのですが、作業は難航し、なかなか取り込めませんでした。

関連記事)
【速報】Qugiyのコードが速攻でやねうら王に取り込まれることになる
https://yaneuraou.yaneu.com/2021/05/05/qugiys-code-will-be-quickly-merged-into-the-yaneuraou/

取り込めなかった理由を書いていきます…が、それぞれの用語を簡単に解説しつつ、順番に話を進めていきます。

Bitboardとは

やねうら王では、Bitboardを用いています。これは、駒のある升に対応するbitが1であるようなbitmap(画像)だと思うとわかりやすいでしょう。将棋盤は9×9 = 81升なので64bitには収まらず、その倍である128bitのbitmapとして扱っています。128bitはSSE2命令だと1命令でandやxorなどの演算が出来るので、高速な重ね合わせの処理などが出来ます。利きの合成に便利です。

例えば、敵陣のbitboardがあって、自分の銀の利きのbitboardがあれば、銀が成れる升を求めるには、その2つのbitboardの(bit単位の)andを行うだけなので一命令で出来ます。

飛び利きはoccupied bitboard依存

また、先後の任意の駒のある升が1となっているbitboardのことをoccupied bitboardと呼びます。ソースコード上は、occなどと略記されることもあります。開発者の間では「occupy(おきゅぱい)」だとか「おっぱい」だとか、呼ばれてるような呼ばれてないような気がします。以下ではoccと書きます。

飛び利きは、先後任意の駒がその途中の升にあると遮断されるので、つまりはocc依存の利きということになります。

Step Effect

occが0(盤上に一切の駒がない)と仮定した時の利きのことをstep effectと呼びます。pseudo attack(仮想利き)とも呼ばれます。やねうら王ではstep effectと呼んでいます。

PEXT × テーブル

やねうら王の飛び利きの処理は、当初PEXT命令を用いていました。

これは、occのうち、step effect(利きが通る可能性のある升)に対応するbitを連続的に並べたものをPEXT命令で作って、それをindexとして表引きするというものです。

step effectは、角が55にあれば16升に利きがあるので、つまりは16bitのbitの組み合わせがあることになります。

// 実際は、端の升には駒があろうとなかろうと、そこまで角の利きは通るので、55の角の利きの影響するのは、12升で、その組み合わせは2の12乗=4096通り。

それぞれの升ごとに表が分かれているような感じなので、(大雑把に計算すると)81升分×4096通り×16byte(==Bitboardのサイズ)ぐらいのサイズのテーブルが必要になり、わりと大きいです。

できればこのような大きなテーブルは使いたくはないです。

Magic Bitboard

2020年2月にRyzen 3990Xが発売になって、ZEN2(Ryzen 3990Xなど)というアーキテクチャでは、PEXT命令が異常に遅いということがわかりました。SNSでもすごく話題になったのでご存知の方も多いかと思います。

そこで、やねうら王もPEXT×テーブルで飛び利きを処理するわけにはいかなくなりました。

仕方なく、やねうら王でも長年導入していなかったMagic Bitboardの導入に踏み切ります。これはチェスのソフトで使われていた技術で、将棋ソフトでは最初にPonanzaが導入し、Aperyがそれに続いたように思います。やねうら王では、PEXT命令があればMagic Bitboardは不要であるという立場であったので、長らく導入してこなかったのですが、その命綱であるPEXT命令を超絶クソ性能にされてしまったのでは、仕方ありません。

Magic Bitboardは、簡単に言うと掛け算をPEXT命令の代わりにするというものです。うまい数を掛け算すると任意のbitを上位のbitに連続するように集めてこれる(ことがある)のでそれを右シフトすればPEXTに近いことができるという原理です。

無論、PEXTの時と同じサイズかそれ以上のサイズのテーブルが必要になります。その初期化コードも大変複雑で、かつ、その乗算に用いる値(magic number)を事前に計算しておかなければならないです。こんなもの、できれば使いたくないです。

ZEN3以降は、PEXTはまともな速度になっているらしく、今後、Magic Bitboardは不要だと思います。しかし世間的にはまだZEN2は現役なのです…。

縦型bitboard

Bitboardは、将棋では128bitの値だという話を上で書きましたが、やねうら王では、先手から見て右上(1筋の1段目)をbit 0、その下の升(1筋の2段目)をbit 1、…というように割り当ててあります。これを縦型bitboardと呼びます。

縦型にしている理由は、香の利きを求めたり、歩の打てる筋を探すのが簡単になるからです。(ある筋に対応するbitが連続するため)

Qugiyの香の利きのアルゴリズム

前置きが長くなりました。やっとQugiyのアルゴリズムの説明に入れます。

まず、後手の香の利きについて説明します。利きの計算にoccが必要なことは上で述べました。

いまsqに置いた後手の香の利きを求めたいとします。occのうち、香のstep effectに相当する升のみに着目します。ここに障害物(任意の駒)があれば、そこで利きは止まります。

step_occ = occ & lanceStepEffect(sq)
// & は bit単位のandを意味するものとします。

縦型bitboardなので、後手の香の利きは利きの方角に進んでいくとその升に対応するBitboardのbitは、それより上位のbitになります。Bitboardを2進数で書くと、下図のようになります。

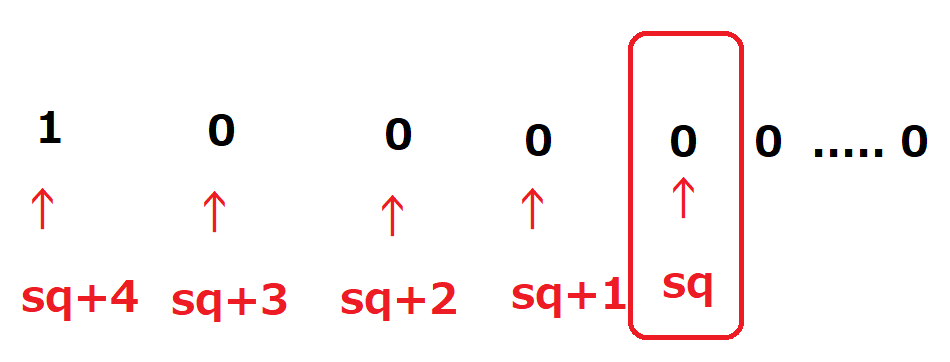
Bitboard上にsqの升に対応するbitがあり、sq+1(先手から見てsqの升の下の升)のbitがその1bit上位にあり、sq+2、sq+3、sq+4と上位には並んでいます。いま、sq+4のところには何かの駒があるものとします。つまりは、このbitはいま1になっており、そこ以外は0となっています。

sqに対応するbitより上の桁だけに着目すれば、2進数で書くと
step_occ = 10000
となっていることになります。

いま、これのbit反転をさせたものを作ります。これはNOT演算で作れます。駒がない部分が1となっているので、すなわち、1のところには利きが通ると解釈できます。
step_occ_not = 01111

そしてsqに対応するbitに1を足します。いま一番下の桁をsqに対応するbitとみているので、要するに1を加算したことになります。そうすると桁が次々と繰り上がり、次のようになります。

step_occ_not + 1 = 10000

つまり、2進数とみなすと駒のある升まで繰り上がり続けるわけですね。

繰り上がりによって値が変化したbitを取り出すには、元のstep_occ_notとXORすれば良いです。XORすることで変化したbitのみが取り出せます。(XORは、0と1か、1と0の時のみ1になる演算なので)

// 実際は、香をsqの升に置いたときsqの升に利きは発生しないので、sqの升に1足すのではなく、sq+1(香にとって歩の利き)に1を足す感じになります。

まとめると、

step_occ = occ & lanceStepEffect(sq);
lanceEffect = (~step_occ + pawnStepEffect(sq)) ^ ~step_occ;

となります。
// ~ はbitを反転するNOT演算、 ^ はXOR演算とします。

これがQugiyの後手の香の利きを求める方法です。

2進数的な加算によって桁あふれが生じて、利きの到達先まで繰り上がっていくというのを利用している点と、XORで変化したbitを取り出すという点がなかなかのアイデアだと思います。この2つのアイデアにより、後手の香の利きが簡単に求まるようになりました。

Qugiyの香の利きのアルゴリズムの改良

私はQugiyのアルゴリズムを加算ではなく減算に変更しました。

減算すると何が起きるかと言うと、桁借りが生じます。例えば、先程のように

step_occ = 10000

である時に、1を引いてやると

step_occ = 01111

となります。つまり、1引くと、最初に障害物に出くわすところまで桁借りが生じて、bitが変化するのです。これをXORで取り出せば良いと考えました。疑似コードで書くと次のようになります。

mask = lanceStepEffect(sq)
step_occ = occ & mask;
lanceEffect = ((step_occ – 1) ^ step_occ) & mask;

さきほどと演算量はほぼ同じですが、先程はpawnStepEffect(sq)という歩の利きテーブルを参照していたのに対して、今回のコードは、-1するだけなのでその部分の表引きが不要になっています。小さな改善ですが、この -1 するという手法は、角の利きを求めるところで再度出てきます。

先手の香の利き

後手の香の利きは終わったので先手の香の利きの話になるのですが、これは上のように加算/減算ではどうにもならないです。bit reverse(bitを逆順にする)命令があれば良いのですが、あまり使いみちのない命令であるせいか、ハード的に実装されているCPUはほとんど存在しないようです。

そこで先手の香の利きは少し泥臭い方法になります。興味のある人は、やねうら王の bitboard.h をご覧ください。

角の利き

角の利きを求めるのにも同じアイデアが使えます。縦型bitboard(盤面の右上がbit 0)である場合、(先手から見て)角の左上と左下方向への利きは、Bitboard的に見て、対応する升が上位bitの方向に移動するので、例えば、左上(もしくは左下)ならば、先程の引き算で後手の香の利きを求めたのと同じコードで求まります。

mask = bishopStepEffect_LeftUp(sq)
step_occ = occ & mask;
bishopEffect_LeftUp = ((step_occ – 1) ^ step_occ) & mask;

つまり、このようにして、左上と左下と右上と右下の4方向をそれぞれ求めてそれを重ね合わせれば良いということです。

AVX2命令(256bitでのANDやXOR演算が一命令でできる)を用いれば左上と左下は同時に求まります。しかし、右上と右下方向は容易ではありません。さきほども書いたようにBitboard的に見て上位bitの方に進んでいく方向ではないからです。

そこで、Qugiyの作者が考えたのは、ここでbyteを逆順にするということです。これがQugiyの3つ目のアイデアです。

byteを逆順にするのはbyte_reverseと呼ばれています。MSVCなら、_byteswap_uint64()命令、GCCなら__builtin_bswap64()命令を使っておれば、適切なCPU命令に置換されます。x86系ならBSWAPというアセンブラの命令で、これはかなり古いCPUでも搭載されていますし、ARM8以降であればREV命令に置換されます。

また、Qugiyのコードでは、SSSE3の_mm_shuffle_epi8命令を用いてxmm(128bitレジスタ)に対して一命令でbyte reverseしています。

byte reverseすると、何が嬉しいかというと、いま、将棋の盤面は縦が9升あり、つまりは9bitあるので、角の右上の利きは必ずbyteをまたぐ(1つのbyteに2升のstep effectが含まれることはない)のです。つまり、byteを逆順にすれば、角の右上、右下の利きは上位bitへ向かう方向になるのです。これにより、後手の香と同じ処理が可能となります。

128bit decrement

AVX2の命令で256bitずつ計算できるのですが、128bit×2とみなして、それぞれをdecrement(1引き算すること)する命令がAVX2には存在しません。64bit×4とみなして、それぞれをdecrementすることはできるのですが…。

そこで、擬似的に128bit decrementを実現せねばなりません。そのためには、下位64bitでの桁借りが生じるなら、上位64bitから 1引いてやる、みたいなコードが必要になります。しかし、AVX2のようなSIMD(単一命令による並列化された)演算では、他のレジスタと加算したりする(垂直演算)のは得意ですが、自分のレジスタ内で加算したりする(水平演算)は苦手です。そのため、このような演算は、実現はできるのですがわりと複雑なコードとなります。

また、AVX2でやるのだから、decrementも同時に2つか4つ行いたいです。

Qugiyの4つ目の工夫がここで出てきます。AVX2のunpack命令を使うのです。これを使って、4方向の利きのBitboard(Bitboard 128bit×4 = 512bit)のうち、各Bitboardの下位64bitだけ集めた、lo(256bitレジスタ)と各Bitboardの上位64bitだけ集めたhi(256bitレジスタ)を用意できれば、このdecrementを4並列でできるというものです。

そのような命令として、AVX2のunpackがあります。つまり、以下のようにして、loとhiを作り出します。

そうすれば、128 bitのdecrement×4並列は以下のように計算できます。

// decrementにおいて、上位64bitに桁借りが発生するのは下位64bitが0の時だけ。ゆえに下位64bitが0なら上位64bitから1を減算すれば良い。

こうして、角の4方向の利きを一気に求めることができるようになりました。

Qugiyが独創的なのは、この4つの素晴らしいアイデア(それぞれは既存のアイデアですが)それらをうまく効果的に組み合わせたことです。

やねうら王にQugiyのコードをすぐに移植しなかったのは何故か？

やねうら王にQugiyのコードを取り込むのは簡単なはずでした。なにせ、テーブルの初期化コードとAVX2のコードは公開されているのですから。ところが、これを取り込むと、非AVX2環境のためにMagic Bitboardのコードは残しておく必要があります。Magic Bitboardのコードはわりと複雑で、そのコードとQugiyのコードとの両方を保守していくのは大変だと判断しました。

また、PEXT命令がZEN2ぐらい遅い環境以外では(ZEN3以降やIntel系など)、Qugiyのコードは本当に速いのかという問題もあります。今後、なくなっていくCPUアーキテクチャのために全力で最適化しても仕方がないという考えです。

そのため、Qugiyのコードをもうちょっと綺麗な形で書き直し、かつ、ZEN3以降やIntel系で以前と変わらない速度が出せて、かつ、ZEN2で高速化して、かつ、AVX2非対応の環境でもMagic Bitboardと同等ぐらいの速度が出てくれないといけないのです。単にQugiyのコードをコピペして持ってくればいいということではないので、これらの実装と検証が大変でした。

結局、多くの方の協力と助言を経て、そのへんの作業がすべてクリアでき、
・Magic Bitboardのコードを完全削除できた
・非AVX2環境でもそれなりに動作する(以前と同等ぐらいの速度)
・ZEN2で+2%程度の高速化
・ZEN3/Intel系でも+1%程度の高速化か、以前と同等ぐらいの速度はでる
というところまで到達できました。

すごく長い道のりで気絶しそうになりましたが、達成できていまはとても満足しています。

ソフトの棋力的には、ZEN2でも+R5程度しか変わっていませんが、Magic Bitboardのような巨大テーブルを使わなくて良いようになったため、メモリ帯域がボトルネックとなるような環境では改善効果が期待できます。(今後、CPUが超many coreになった時に利いてくるかも？)