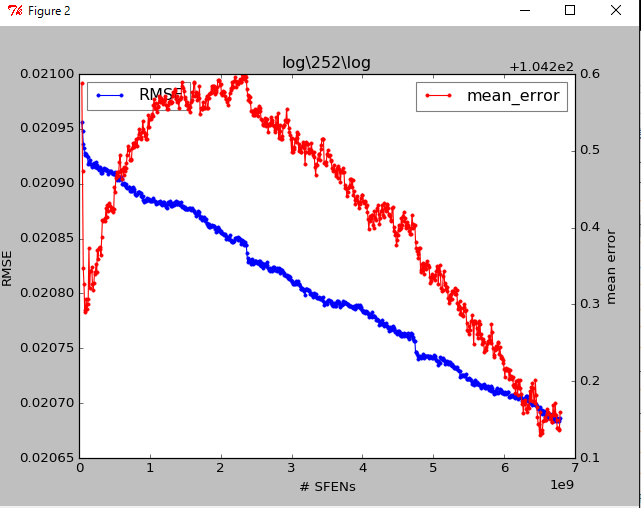
やねうら王ライブラリを用いて、雑巾絞りがうまく出来ているときは、概ね以下のようなグラフになります。(使用教師局面数 = 20億)
rmse(Root Mean Squared Error:平均二乗誤差の平方根)とme(Mean Error:平均誤差)ですが、前者は綺麗に減衰していき、meは最初少し上がるのですが、そのあとなだらかに減衰します。
※ ダミーデータを使って描いたグラフなので、rmseとmeの値は適当です。
この可視化ツールは、たぬきチームの方に作っていただいたpythonスクリプトで、やねうら王のGitHubのscriptフォルダに入っています。(活用してみてください)
・meが何故いったん上がるのか?
・rmseは20億局面ごとに断崖絶壁のように急降下しているのは何故か?
という質問にお答えしておきます。
後者は、シャッフルが先読みしている分(20M局面程度)でしか行わないためです。rmseの計算に使っている局面に類似した局面がそのあたりに分布しているので、それを学習に使った瞬間、見かけのrmseは急激に下がるという理屈です。知らないと気づきにくい現象ですが、機械学習ではそういうこともあるということで…。
meのほうがいったん上がるのは、AdaGradの性質と言えなくはないですが、上に書いた理由もあって、元の値から一時的に下がって見えていただけというのもありそうです。
また、rmseがこれより上下に大きく振動している場合は学習率を下げるか、mini batchのサイズを調整するかしたほうが良いでしょう。
原理的にはmini batchのサイズを大きくしたほうが勾配が正確に出るので大きくしたいのですが、しかしそうすると一度に変動する量が大きくなるので学習率を下げないといけなくて、学習が進むのが遅くなります。そのへんを上図のようなrmseのグラフを見ながらうまく調整してみてください。

やねうら王のscriptフォルダに入れているかと思ったら入れてなかった…。次回の更新のときに入れておきます。tanukiのGitHubのほうに同じファイルがあるはずなので、急ぎの方はそちらをお使いください。
「誤差」が何を意味するのか分かりませんが、以前「真やねうら王で雑巾しぼり上手くいかなかった原因判明」とか言ってたからみなのでしょうか?
誤差は、教師(前の評価関数による深い探索での評価値 = d)と、(現在学習中の評価関数パラメーターでの)浅い探索での評価値(= s)との差を誤差と言います。ただし、rmseのほうは一致度を見るためにシグモイド関数を通してます。
そんなわけで、やねうら王では、シグモイド関数をσとすると
me = Σ abs( d – s )
rmse = sqrt ( Σ (σ(d)-σ(s))^2 )
となります。
コンピュータ将棋界ではAdaGradが主流なんですか?
技巧とたぬきは違いましたっけ…
やはり実装が楽だから?それともライブラリソフトのせい?
余談ですが例のdeep learningの本注文したら日本語能力検定の演習本が届きましたよ…
deep learningせずに日本語勉強しろということですかAmazonさん…
> コンピュータ将棋界ではAdaGradが主流なんですか?
aki.さん(ponanzaチームの下山さん)がお勧めしているというのもありますが…。
http://qiita.com/ak11/items/7f63a1198c345a138150
1. Adamより保持しておくパラメーターが少ない(省メモリ!)
2. ハイパーパラメーターとして学習率が一つだけ!
3. 挙動がわかりやすく、制御しやすい。
という観点から、私もお勧めです。
> 余談ですが例のdeep learningの本注文したら日本語能力検定の演習本が届きましたよ…
ワロタw