前回の続き。今回は、駒の置かれている升に利きがある時の価値を考えてみます。
駒×味方の利き
駒のある升の味方の利き(駒が先手の駒であれば先手の利き)がある時にその価値を調べてみます。
駒に味方の利きがあれば(俗に言う「駒に紐がついている」状態)タダ取りされないので、駒の価値に比例する価値が、その利きにはあると考えられます。
そこで、加点するとして、
piece_value(駒の価値)× X / 1024
のXの部分をoptimizerに尋ねてみたのですが、この値が小さすぎるんです。1024だと計算精度が不足しているようでしたので、分母を4096にしてみました。そうすると、optimizerは X = 33 と返してきました。
駒に味方の利きがある時の価値:
piece_value × 33 / 4096
というわけです。
値小さすぎない?
歩の価値は90なので、歩の場合、90×33/4096 = 0.725です。1点にも満たない価値です。評価値の計算自体は、前回記事に書いたように32倍して計算することにしたので、評価値には乗っているでしょうけども、非常に小さい値です。
前回記事にあるように、将棋ベーシックが駒に味方の利きがあれば1点加点していたのはわりと正しくて、味方の利きがある歩に対して2点以上加点すると弱くなることがわかりました。
利きの数によって価値はどう変わる?
ある駒に味方の利きが2つある時は、さきほどより価値があるのでしょうか?
optimizerに尋ねてみると、
駒に味方の利きが2つある時の価値:
piece_value × 43 / 4096
と返ってきました。わずかですが、2つ利きがあるほうが価値が高いようです。
味方の利きの評価でどれだけ強くなる?
+R10ほど強くなりました。
駒×相手の利き
駒に相手の利きがある時、これは将棋では「質駒(しちごま)」と呼ばれ、「質(しち)に入っている」(いつでも取れる)状態を意味します。
そこで、自駒に相手の利きがある場合、大きなペナルティがあるはずで、これも駒自体の価値×係数 みたいなペナルティが発生していると考えられます。
また、相手の利きが1つの場合と2つの場合とで、それを回避しやすさが異なります。
いまは評価関数では手番を考慮していないのですが、仮に自分の手番だとして、自駒に利きをつけている相手の駒が1つであれば、その駒を取ったり、利きを遮断したりできます。ところが利きが2つですと、相手の駒を取ったり、利きを遮断したりして、1手で対象駒への利きの数を0にすることはできなくなります。
ということは、相手の利きは1つより2つのほうが大きなペナルティがあるはずです。
このペナルティの大きさをoptimizerに聞いてみました。
駒に相手の利きが1つある時のペナルティ:
piece_value × 113 / 4096
駒に相手の利きが2つ以上ある時のペナルティ:
piece_value × 122 / 4096
あまり違いはないですが、後者のほうが1割ほど多いですね。
角が質に入っている時のペナルティは1歩損の1/8
角の価値は、第一回で出てきたように855です。(歩の価値を90とする)
角が質に入っている(相手の利きが1つある)場合、上の計算式ですと
855 × 113 / 4096 ≒ 23.6
だけペナルティがあることになります。
1歩得は歩の価値の倍 = 90×2 = 180ですから、角が質に入っていると、1歩損の1/8ぐらいの損であるということです。
今回のソースコード(抜粋)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
// 駒に味方/相手の利きがn個ある時の価値(この係数×駒の価値/4096が上乗せされる) int our_effect_to_our_piece[3] = { 0, 33 , 43 }; int their_effect_to_our_piece[3] = { 0, 113 , 122 }; (中略) // さらにこの駒に利きがある時は、その利きの価値を上乗せする。 // 味方の利き(紐がついてる) = 加点 // 相手の利き(質(しち)に入っている) = 減点 // piece_valueは、後手の駒だと負の値になっている。 // scoreはいま先手から見たスコアを計算しているのでこれで辻褄は合う。 int effect_us = color_of(pc) == BLACK ? m1 : m2; int effect_them = color_of(pc) == BLACK ? m2 : m1; score += piece_value * our_effect_to_our_piece [effect_us] / 4096; score -= piece_value * their_effect_to_our_piece[effect_them] / 4096; |
相手の利きの評価でどれほど強くなる?
+R15ほど強くなりました。
何の駒の利きであるか問題
そうは言っても、角が歩で取られそうなのと飛車で取られそうなのとは全く意味が異なります。
利きの数には、何の駒による利きなのかは区別がないので、利きをつけている駒が一緒くたになっています。
さきほどの例では、角に相手の利きがある時、その利きをつけている駒ごとにペナルティの大きさは本来異なるはずで、それを均した値が 113/4096 だということです。
しかし、いま、KKPEEテーブルは、対象升の利きの数しか見ていないので、それが何の駒による利きなのかはわかりません。よって、利きのつけている駒ごとにペナルティを調整したくとも、KKPEEテーブルではそれはできないということです。
KPPのような3駒関係ですと、近接駒(長い利きを持っていない駒)は、どの駒による利きがその駒に当たっているかはわかるので、この部分は正確に計算できていると考えられます。
ただし、KPPでは、ある駒に相手の駒が複数利いている時は、過剰にそれを評価していることになります。上の例で見たように、相手の利きが1つの場合と2つの場合は10%しかそのペナルティは違いません。2つの利きがある時、これを1つの場合の2倍のペナルティにしてしまうのは、過剰にペナルティを与えていることになります。
まあ、実戦で複数の駒が利いている局面は稀なので、そこで多少評価に誤差があっても…という意味はあります。
手番問題
相手の利きがある場合、自分の手番である場合とそうでない場合とでは話が違ってきます。
そこで、KKPEEテーブルにも手番を導入して(テーブルサイズは2倍になる)、KKPEET(TはTurn = 手番の意味)テーブルにしたほうが良いのですが、optimizerですべてのパラメーターを調整しなおす必要が出てきます。
私のほうでoptimizerで一つのパラメーターを求めるのに、AWS換算で3000円ぐらいのお金がかかっています。この連載記事、ここまでで、すでにAWS換算で20万円ほどかかっています。電竜戦の準備のためには1万円ほどしか使ってないのに、です。
そんなわけでして、KKPEETテーブルにすれば確実に強くなることはわかっているものの、本連載記事ではやりません。
ちなみに、このように無駄にお金を使い続けているやねうら王プロジェクトのための贈り物はいつでもお待ちしております。→ http://yaneuraou.yaneu.com/amazon%e3%82%a6%e3%82%a3%e3%83%83%e3%82%b7%e3%83%a5%e3%83%aa%e3%82%b9%e3%83%88/
評価関数の仕事と探索の仕事について
「次に駒が取られる」という状態を評価関数の側で頑張るのはあまり筋がよくないのです。何故なら、探索のほうで1手読めば済む話だからです。評価関数を重くして、1手先の評価が早くわかることにあまり価値はないのです。
評価関数の設計に慣れていない人は、より正確な評価を求めて、評価関数に何でもかんでも詰め込もうとして、「評価関数が2倍遅くなるけど、1手早く評価値がわかる」みたいな評価関数を作ってしまいます。
しかし、これは明らかに損なのです。探索で1手深く読むために2倍も時間がかからないので(たぶん現在の探索技術だと1手深く読むために必要な時間は1.3~1.8倍とかそんなもの)、1手読めばわかることを評価関数で正確に返すために評価関数が2倍遅くなるのは、全く割りに合わないのです。
では逆に評価関数は何をやってくれればいいかというと、ずっと先にならないとわからないような評価をして欲しいのです。例えば、囲いの堅さです。囲いが崩されるのは終盤なので、探索がいくら頑張っても序盤の局面で、終盤まで読めるわけはなく、囲いの堅さを評価するのは評価関数の仕事です。
それから、駒のpositionalな(位置の)評価です。これも、次の1手でその駒を動かすとは限らないので(最悪、そのまま何十手も動かさないこともある)、探索のほうで頑張っても不正確な価値となってしまいます。
このように評価関数は1手先の期待値を返すように努力するのではなく、探索に任せるべきところは探索に任せて、なるべく先の局面の期待値を返すように努力すべきなのです。
そういう意味からすると、例えば「角が歩で取られそう」みたいな局面は探索の側がその取り合いが終わった局面までは延長して調べてくれるでしょうから、「角が歩で取られそう」なことを対してそれをなるべく正確に評価しようと評価関数があまり頑張っても仕方ない意味はあります。
逆に「金が角で取られそう」というのは、取る側は駒損になりますから、探索でも見落とされがち(&すぐに取るとは限らない)なので、こういうのは評価関数で正しく評価したほうが良いです。(今回のKKPEEでは、これが評価できませんが。)
おい、たけわらべ、金銀が逆だぞ問題
たけわらべは、金冠によくやってしまいます。この連載で作ってきたソフトも、金冠にわりとしてしまいます。

金冠にした時の利きの価値を計算してみましょう。利きの価値は、王様からの距離に反比例するので(1つの升に複数あると少し価値が減りますが計算がややこしくなるので、それはいま考えないことにします)、以下のようになります。
・金冠の時
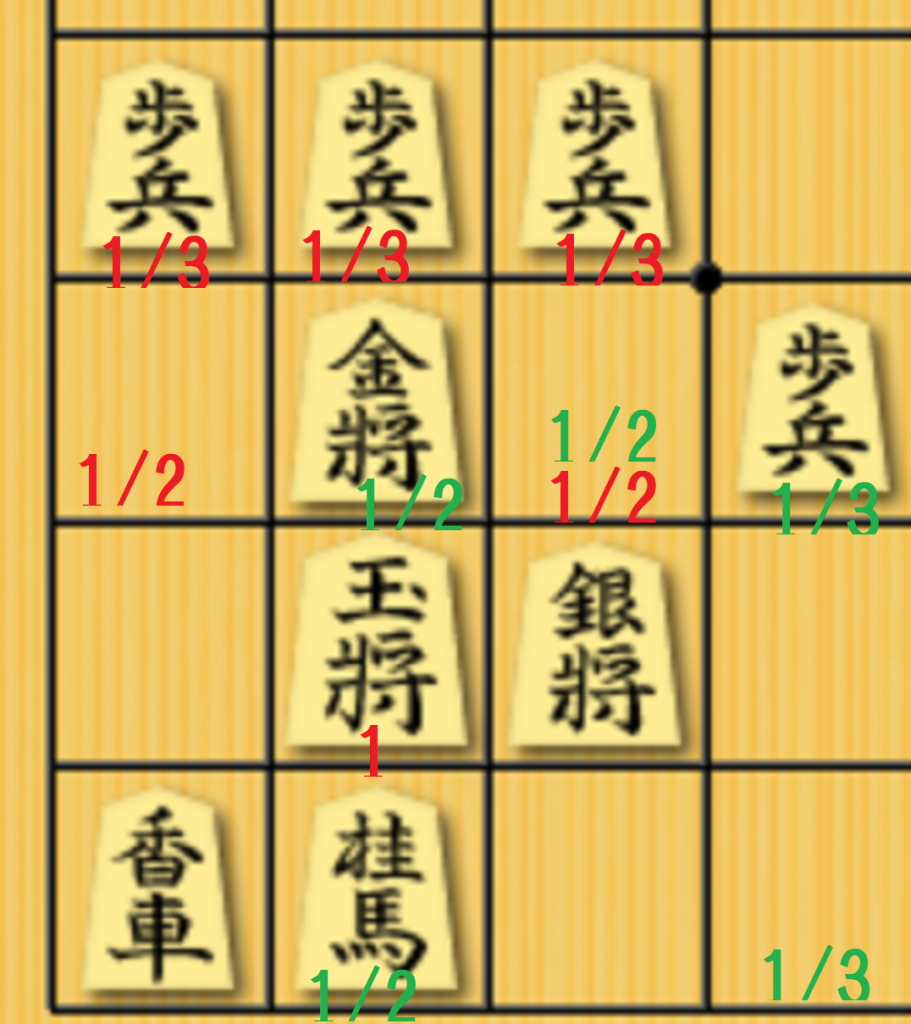
金の利きの価値(赤文字)に関しては、
1 + 1/2 × 2 + 1/3 × 3 = 3
です。
銀の利きの価値(緑文字)に関しては、
1/2×3 + 1/3×2 = 2 + 1/6
合計 ≒ 5.16
・銀冠の時
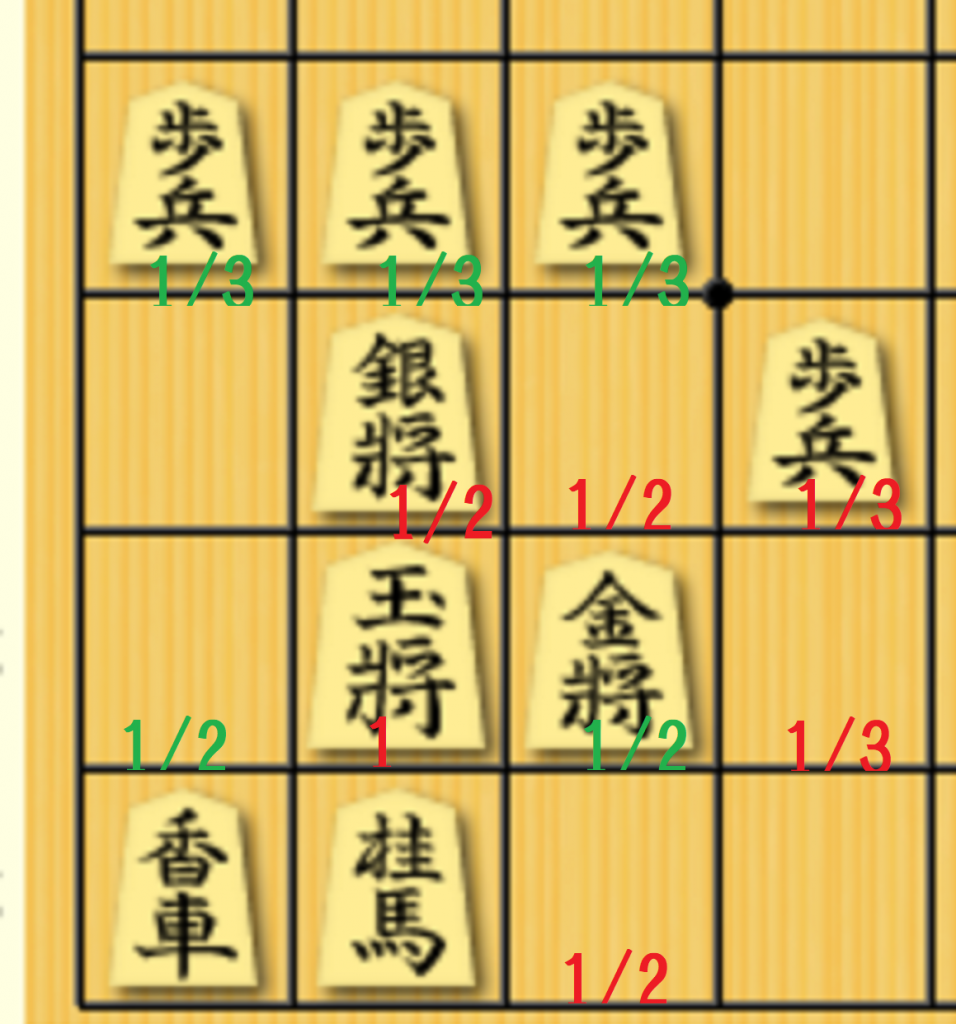
金の利きの価値
1 + 1/2×3 + 1/3×2 = 3 + 1/6
銀の利きの価値
1/2×2 + 1/3×3 = 2
合計 ≒ 5.16
なんと、同じなのです。
ここにさらに相手玉への脅威(相手玉に対する金と銀の利きの価値)を計算すると、金冠のほうが相手玉に近いところに利きをより多く発生させているので(金は横に利くので)、相手玉への脅威は、金冠のほうが上です。
総合すると金冠のほうが価値が高いことになってしまいます。そりゃ、たけわらべも好んで金冠にするのも無理はないですね。
これは、我々の利きの評価の仕方が何か間違っているのでしょうか?それとも何か欠けている特徴量があるのでしょうか?
金冠は何故悪形なのか?
金冠が何故悪形なのか考えてみましょう。将棋指し(有段者)ならば、金冠が悪形であることはその理由も含めて言えるはずです。
理由1) 銀に紐がついていない(王様以外の利きがない)
現状、利きの数は王様の利きも含めて計算していますが、理由1は、玉周辺の駒に関しては王様の利きを除いた数で計算する必要があることを示唆しています。
理由2) 王様の右下の升が空いているのに、ここに利きがない
右下の升には王様以外の利きがないで、終盤においてこの升から駒を放り込まれる手が常に見えています。このように玉の8近傍の升が空いていて、かつそこに王様以外の利きがない場合にはペナルティを課すべきだということを示唆しています。
他にもたくさん理由はありますが、とりあえず大きな理由はこの2つでしょう。
今回のソースコード
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
// 【連載】評価関数を作ってみよう!その8 : http://yaneuraou.yaneu.com/2020/11/30/make-evaluate-function-8/ // 駒に味方の利きがあるときは加点 (+R10) // 駒に相手の利きがある時は減点(+R15) // KKPEEテーブル。Eが3通りなのでKKPEE9と呼ぶ。 // 利きの価値を合算した値を求めるテーブル // [先手玉の升][後手玉の升][対象升][その升の先手の利きの数(最大2)][その升の後手の利きの数(最大2)][駒(先後区別あり)] // 81*81*81*3*3*size_of(int16_t)*32 = 306MB // 1つの升にある利きは、2つ以上の利きは同一視。 int16_t KKPEE[SQ_NB][SQ_NB][SQ_NB][3][3][PIECE_NB]; // ↑のテーブルに格納されている値の倍率 constexpr int FV_SCALE = 32; void init() { // 王様からの距離に応じたある升の利きの価値。 int our_effect_value[9]; int their_effect_value[9]; for (int d = 0; d < 9; ++d) { // 利きには、王様からの距離に反比例する価値がある。 our_effect_value[d] = 83 * 1024 / (d + 1); their_effect_value[d] = 92 * 1024 / (d + 1); } // 利きが1つの升にm個ある時に、our_effect_value(their_effect_value)の価値は何倍されるのか? // 利きは最大で10個のことがある。格納されている値は1024を1.0とみなす固定小数。 // optimizerの答えは、{ 0 , 1024/* == 1.0 */ , 1800, 2300 , 2900,3500,3900,4300,4650,5000,5300 } // 6365 - pow(0.8525,m-1)*5341 みたいな感じ? int multi_effect_value[11]; for (int m = 0; m < 11; ++m) multi_effect_value[m] = m == 0 ? 0 : int(6365 - std::pow(0.8525, m - 1) * 5341); // 利きを評価するテーブル // [自玉の位置][対象となる升][利きの数(0~10)] double our_effect_table [SQ_NB][SQ_NB][11]; double their_effect_table[SQ_NB][SQ_NB][11]; for(auto king_sq : SQ) for (auto sq : SQ) for(int m = 0 ; m < 3 ; ++m) // 利きの数 { // 筋と段でたくさん離れているほうの数をその距離とする。 int d = dist(sq, king_sq); our_effect_table [king_sq][sq][m] = double(multi_effect_value[m] * our_effect_value [d]) / (1024 * 1024); their_effect_table[king_sq][sq][m] = double(multi_effect_value[m] * their_effect_value[d]) / (1024 * 1024); } // 駒に味方/相手の利きがn個ある時の価値(この係数×駒の価値/4096が上乗せされる) int our_effect_to_our_piece[3] = { 0, 33 , 43 }; int their_effect_to_our_piece[3] = { 0, 113 , 122 }; // ある升の利きの価値のテーブルの初期化。 // 対象升には駒がない時の価値をまず求める。(駒がある時の価値を計算する時にこの値を用いるため) // そのため、Pieceのループを一番外側にしてある。 for (Piece pc = NO_PIECE; pc < PIECE_NB; ++pc) // 駒(先後の区別あり) for (auto king_black : SQ) for (auto king_white : SQ) for (auto sq : SQ) for(int m1 = 0; m1<3;++m1) // 先手の利きの数 for (int m2 = 0; m2 <3; ++m2) // 後手の利きの数 { // いまから、先手から見たスコアを計算する。 double score = 0; // 対象升(sq)の利きの価値。 // これは双方の王様から対象升への距離に反比例する価値。 score += our_effect_table [ king_black ][ sq ][m1]; score -= their_effect_table[ king_black ][ sq ][m2]; score -= our_effect_table [Inv(king_white)][Inv(sq)][m2]; score += their_effect_table[Inv(king_white)][Inv(sq)][m1]; if (pc == NO_PIECE) { // 1) 駒がない対象升 } else if (type_of(pc) == KING) { // 2) 玉がいる対象升 } else { // 3) 玉以外の駒がいる対象升 // 盤上の駒に対しては、その価値を1/10ほど減ずる。 // 玉に∞の価値があるので、PieceValueを求めてその何%かを加点しようとすると発散するから玉はここから除く。 double piece_value = PieceValue[pc]; score -= piece_value * 104 / 1024; // さらにこの駒に利きがある時は、その利きの価値を上乗せする。 // 味方の利き(紐がついてる) = 加点 // 相手の利き(質(しち)に入っている) = 減点 // piece_valueは、後手の駒だと負の値になっている。 // scoreはいま先手から見たスコアを計算しているのでこれで辻褄は合う。 int effect_us = color_of(pc) == BLACK ? m1 : m2; int effect_them = color_of(pc) == BLACK ? m2 : m1; score += piece_value * our_effect_to_our_piece [effect_us] / 4096; score -= piece_value * their_effect_to_our_piece[effect_them] / 4096; } // 先手から見たスコア KKPEE[king_black][king_white][sq][m1][m2][pc] = int16_t(score * FV_SCALE); } } // KKPEE9 評価関数本体(わずか8行) // 変数名短くするなどすれば1ツイート(140文字)に収まる。 Value compute_eval(const Position& pos) { Value score = VALUE_ZERO; for (auto sq : SQ) score += KKPEE[pos.king_square(BLACK)][pos.king_square(WHITE)][sq] [std::min(int(pos.board_effect[BLACK].effect(sq)),2)][std::min(int(pos.board_effect[WHITE].effect(sq)),2)][pos.piece_on(sq)]; // KKPEE配列はFV_SCALE倍されているのでこれで割ってから駒割を加算する。 score = score / FV_SCALE + pos.state()->materialValue; return pos.side_to_move() == BLACK ? score : -score; } |
次回予告
次回「王様の右側にいる銀について、王様以外の利きがないからとペナルティを課したら弱くなったんですけど?」です。お楽しみに!

評価関数の仕事と探索の仕事、とてもわかりやすい一節でした。
金冠の考察もいい引きですね!
あと2,3回で最終回でございます。最後は衝撃の結末が待ってるです。
> 相手玉への脅威は、金冠のほうが上です。
> そりゃ、たけわらべも好んで金冠にするのも無理はないですね。
ここで別のものを想像してしまってツボにはまったw
別のものとは?
互換性のありそうなものとして、液体○ヒとか○ナコー○とか?
他にもアン○ルツとかℓ-メントールが含まれていそうなもの全般でw
ああ、虫刺されの「キンカン」ね。あれ、発売元が株式会社金冠堂なんだけど、将棋指しはあれ聞くと「なんか横から攻められたら弱そうな会社やなぁ」ぐらいの感想しか出てこない。
じゃああとそれと、それを右手に持って突き進むモーゼ様。
それから、それ系の薬の容器で、先端のスポンジに含浸してる量が足りなくて肌に押し付けているけど、うまく弁が開かなくて仕方なくスポンジを指で押したら、中の薬液が一気に出てきて自分の玉付近に垂れ落ちた、というときに発生する事象もw
他の記事とかツイート読んでないとわからんコメントをすると、あとからこの記事だけ読みに来た人が、わけわからんってなるのでほどほどに頼む。
金冠と銀冠が同じw
ときどきソフトが早指し(ミリ秒単位)で
elmo囲いの銀と金を逆にして囲うのも
その辺りの評価に
手が回らなかったということですかね
金冠等の上段金は斜めに動いた際に自囲いへの効きが弱くなるというのも悪形とされる理由になりそうでしょうか。
| ・ ・v桂 ・
| 歩 歩 ・ ・
| ・ 金 桂 ・
| ・ 玉 銀 ・
こんな感じで攻められ斜めに逃げた場合、自陣への効きが減るので銀冠よりも価値が大きく下がるとも見れますかね?
本稿の例でいえば、
87金→76金(3-23/12=13/12)
87銀→76銀(2-19/12=5/12)
ただ「金が斜めに誘われた場合」を評価するのって評価関数より探索の領分じゃない?とも…
悪形である理由が色々と言える以上、評価関数は、それを評価してほしいものですね。