今回は、NNUE評価関数の一番シンプルな形で何故穴熊に囲えるのかについて解説してみます。
まず、ニューラルネットの入力層には、K(玉の位置)とP(それ以外の駒に振られた通し番号)があります。その駒が存在するところは1、存在しないところは0となっています。
例えば穴熊で自玉が9九、自分の銀が8八にいるのでしたら、入力層の9九玉に対応するユニットには1が現れています。同様に8八銀に対応するユニットには1が現れています。話を単純化するためにその他の駒は存在せず、それらの入力ユニットの値は0だとしましょう。
NNUEでは、これが全結合で次の層とつながっています。つまり、全部が配線されているということですね。いま、9九玉と8八銀以外の入力ユニットは0なので、次段のユニットへの入力もそこからの配線に関してはすべて0になります。なので、以下にはそこは省略した図をかきます。
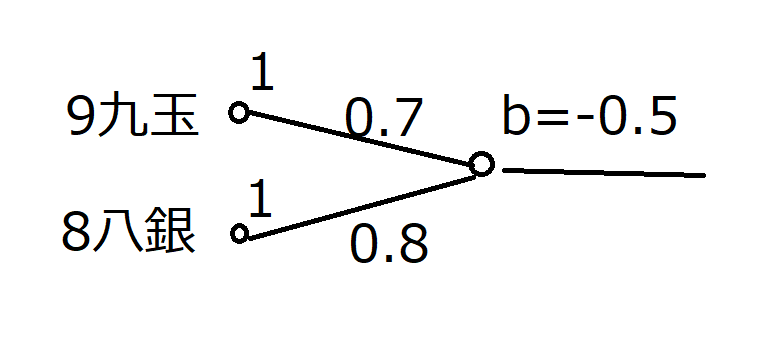
図の0.7というのは重みです。掛け算するときの係数だと思ってください。bというのはbiasで、これはそのあとに足し算するオフセット値(下駄履きさせる値)だと思ってください。
つまり、1段目の図のニューロンへの入力は、
1(9九玉)×0.7 + 1(8八銀)×0.8 – 0.5 = 1.0
となります。
このニューロンが値を出力するときに、入力された値に対して活性化関数というのを通します。
NNUEでは活性化関数を ReLUとしています。ReLUはヒンジ関数と呼ばれるもので、ReLU(x) = max(0,x)となります。要するにマイナスの値を入力したときに0を出力して、そうでなければ元の値をそのまま出力するという関数です。
いま入力が1.0なので、出力も1.0となります。
つまり、このニューロンは9九玉に対する8八銀の価値を非常に評価していて、この2つが同時に出現したときに1.0を出力します。片側だけが出現した場合ですと、例えば9九玉が出現して、8八銀が出現していないならば、
1(9九玉)×0.7 + 0(8八銀が出現していない) × 0.8 – 0.5 = 0.2
となります。
うまくこの重みとbiasの値を調整すれば、特定の2駒が出現しているときのみ1を出力して、さもなくば0を出力するニューロンが作れます。(挑戦してみてください!)
なるほど、この穴熊ニューロンがあれば、穴熊に囲えそうだというのが見えてきました。
全結合においては、2駒のみならず、特定の3駒が出現したときにのみ1を出力するニューロンも作ろうと思えば作れます。(これも挑戦してみてください!)
ということは、「NNUEは三駒関係(KPPT型評価関数)を包含するのか」という話になるのですが、NNUEでは1層目のユニット(ニューロン)の数は、256しかありません。1層目では(最大でも)256個分しか3駒関係を表現できません。三駒関係の組み合わせは81升(玉の位置)×P(1500通り程度)×P(1500通り程度)/2 ≒ 1億程度あります。1億に対して256って少なすぎません?
どう見ても三駒関係の上位互換ではなさそうです。
では三駒関係に対して何が優れているのでしょうか?(次回記事に続きます)

活性化関数にシグモイド関数を使うと上手くいかないのでしょうか
ReLUが必須条件だとすると、ReLUが有効だとわかったのが2011年
3駒関係が開発されたのは2006年だから、3駒の後になったのは歴史の必然のような気がします
> 活性化関数にシグモイド関数を使うと上手くいかないのでしょうか
3層しかないのでシグモイド関数でもバックプロパゲーション時の勾配消失問題は起こらないのでまあ関係ないのでは…。
シグモイド関数の計算は少し嫌ですけども、当時の環境(32bit OS + SIMDなし)ですとたぶん前段からの入力10bit , 重み8bitとかにして表引きで解決するような気がするので、まあ、あまりそこは問題でもないような。
> 特定の2駒が・・・(挑戦してみてください!)
こういうことでいいのでしょうか???
1(9九玉)×1.0 + 1(8八銀)×1.0 – 1.0 = 1.0 → ReLU( 1.0) = 1.0
0(9九玉)×1.0 + 1(8八銀)×1.0 – 1.0 = 0.0 → ReLU( 0.0) = 0.0
1(9九玉)×1.0 + 0(8八銀)×1.0 – 1.0 = 0.0 → ReLU( 0.0) = 0.0
0(9九玉)×1.0 + 0(8八銀)×1.0 – 1.0 = -1.0 → ReLU(-1.0) = 0.0
ですです(`・ω・´)b
一段目に256×2個のニューロンがありますけど、
その中の1個が例えば、例えばですよ真ん中の下の方に玉があって、その堅さ。だから、6八玉とか5八玉とか4八玉とか6八金とか5八金とか4八金とか。そういう玉の堅さを表現するとかなら理解できます。
しかし、残りの255個や2段目や3段目は何しているのか全く分かりません。「その2」を「わくてか」しながら待っています。
> そういう玉の堅さを表現するとかなら理解できます。
そんな感じだと思いますよ。(`・ω・´)b