前回記事の続きをやっていきましょう。
前回、入力をK(玉のある升 81通り) + P(玉以外の駒の種類・升を表現した通し番号 1548通り)として、1つのニューロンで穴熊に囲えるということを説明しました。
これは、99玉 + 88銀 + 89桂 + 79金のような複数の駒が特定の位置関係にあるときに発火する(1を出力する)ニューロンが作れることの証明でもありました。
このことは、入力(K + P)と隠れ層の1層目との間が全結合である場合、戦型判定が1層目のたった1つのニューロンで表現出来ることを意味しています。
例えば振り飛車 42飛 + 76歩 + (77角 or 88角)の組み合わせが出現したときにのみ1を出力して、さもなくば0を出力するニューロンを作ることができます。
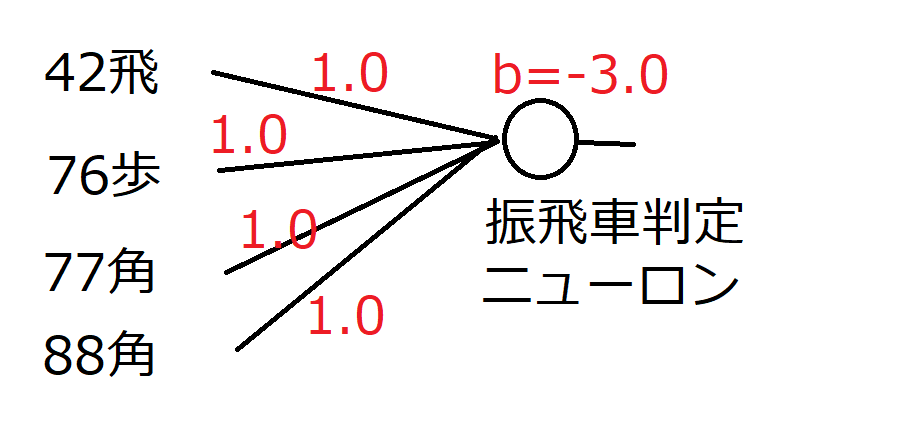
(図の意味は前回同様なので説明は省略)
では、振り飛車のときの78銀には0.1点加点、67銀に0.2点加点、56銀には0.3点加点するにはどうすれば良いでしょうか?
これは、(人間がパラメーターを調整するとしたら)まずその戦型において加点したいニューロンを1層目に用意します。
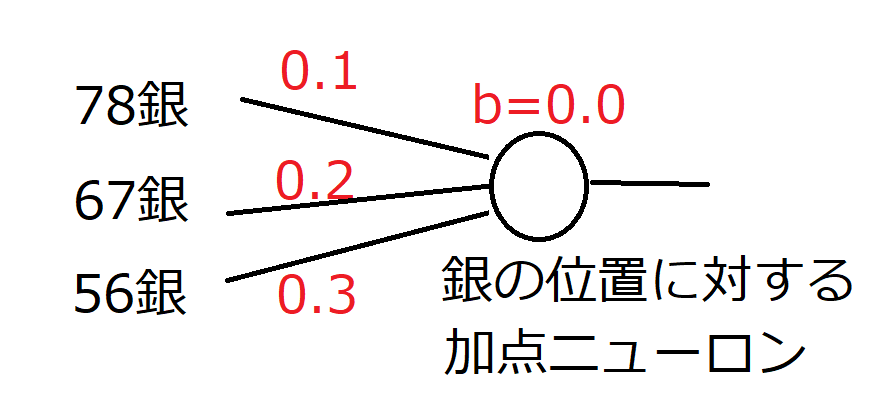
前者と後者を組み合わせると、振り飛車のときに78、67、56それぞれの位置の銀に対して加点することができます。
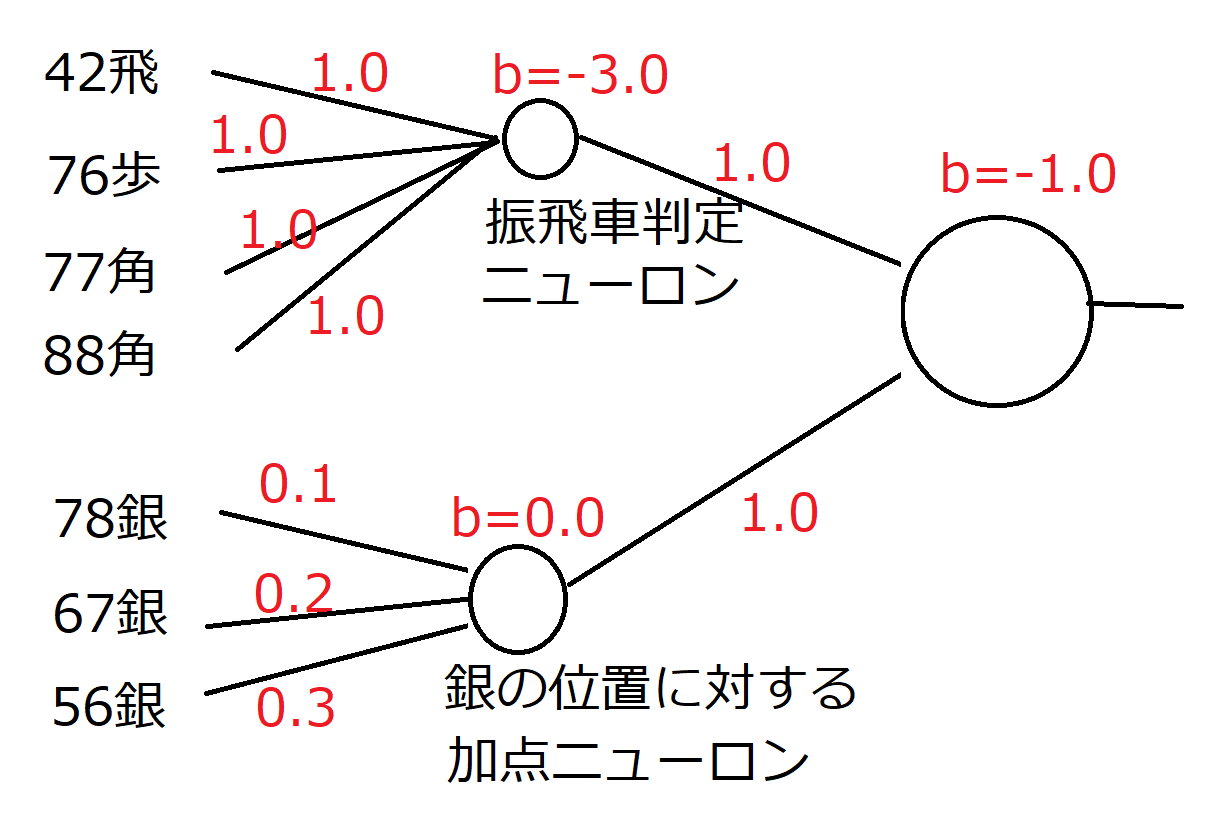
つまり全結合であれば、隠れ層2層、1層目が2 Unit、2層目が1 Unitで戦型判定+その戦型に対する駒の配置の良し悪しに対して加点できることが証明されました。(今回の場合、隠れ層の1層目と2層目との間は全結合でなくても良いですが..)
このことから、NNUE評価関数は戦型把握とその戦型に対する駒の配置の学習能力について大変優れていると推測できます。
これは、全結合型の利点だと言えます。同じニューラルネットを用いた評価関数であっても全結合を基本的に用いないタイプのネットワーク構成ですと、このような戦型判定は難しくなります。(例えば、AlphaZeroはResNetですが、このような戦型判定を学習するのはわりと難しいのではないかと思います。)
まあ、もっとも、その戦型判定が頻出する形(居飛車・振り飛車・角換わり)程度であれば良いのですが、それ以上の特殊な形を学習しても、戦型を誤判定して駒の配置に対して変な加点をしてしまいそうですから、なかなか難しいところです。
とりあえず、今回の結論としては、NNUE型評価関数は従来の評価関数(KPPT型)と比べると戦型を正しく判定できるのでより高い精度で駒の配置に加点ができるという特徴を持っていて、それが強さの秘密なのでは?ということです。
一方で、学習に用いた教師に出現しないような戦型をNNUE型で評価させるとき、戦型を誤判定して、駒の配置に対して変な加点をしてしまい、そのときはKPPT型より(真の期待勝率から)誤差の大きな評価になってしまうのではないかと思います。
そういう意味では、NNUE型にはKPPT型よりもさらに偏った形で得意な局面と不得意な局面が存在することになり、ソフトごとの相性がわりと表面化するのではないかと予想されます。(データを採ったわけではないので私の単なる予想です。)
次回記事に続きます。

稲庭将棋復活か?
ΩΩΩ<な、なんだってー!?
稲庭将棋、R3500を超えた相手には普通に位取りされて手筋連発されて一気に崩壊するみたいですけどね…。
あの戦法を改良すると、もしかすると通用する可能性はありますが…。
もやもや~とした曖昧な評価ができるので、「なんか自玉&敵玉がヤバソウな雰囲気」の時と「自玉&敵玉は安全な雰囲気」で打ち分けれるのかな?
序盤と終盤で評価関数変えようみたいなのから超パワーアップした感じの?
良く分からんけど。
> 序盤と終盤で評価関数変えようみたいなのから超パワーアップした感じの?
超パワーアップになるか、(計算量が増えて)超パワーダウンになるかはわかりませぬ…。(´ω`)
戦型の識別能力は高いので特定の戦型だけを学習させるなら、KPPTなんかよりはよほど強いのでしょうね。
すごく分かりやすい記事でした。
少し気になったのは振り飛車の例のところは後手の振り飛車に対する先手の陣形ってことでしょうか?
(ただの符号ミスだったらすいません)
Oh..「68飛」のつもりで「42飛」と書いてました。(;ω;)
画像なので修正面倒なので修正しませんが…。申し訳ありません。