前回記事の続きです。
NNUE型がそんなに戦型判定について優れているのなら、戦型ごとに良い指し手(良い駒の配置)を学習することが出来そうですし、同様に序盤の指し手(良い駒の配置)と中終盤の指し手(良い駒の配置)をそれぞれ分けて学習させれば、さらに強くなるのでは?と考えるのは自然なことです。
かつてKPPT型でも序盤と中終盤とで評価値を分けて計算して、それを内分してその局面の評価値を出そうという試みがありました。(e.g.2013年ごろの『Ponanza』)
しかし、それはあまり強くはならなかったようです。その両方を計算するコストが馬鹿にならないのでしょう。
そもそもKPPT型でも玉の位置ごとに異なるテーブルを参照しているような形になっているので(評価値 = Σ kpp[k][p1][p2]みたいな形なので)、中終盤で入玉が絡むのであれば、玉は普通中段より上に位置しており、それは別のテーブルを参照していると言えます。なので、あえて序盤と中終盤とで分ける必要はなかったと言えるでしょう。
NNUE型でも標準的なNNUEはhalfKP型で、Kの位置ごとに異なるテーブルを参照していると言えるので、入玉に関しては異なるテーブルを持っていると言えなくはありません。なので、このことから、序盤と中終盤とで別のテーブルを参照していると言えなくはありません。
しかし、現在のgamePly(初期局面からの手数)を評価関数で用いているニューラルネットの入力として用意してやれば、より学習がうまくいくのではないかというのは誰もが思うところです。
dlshogiの山岡さんが入力の特徴量としてgamePly(下記記事ではTotal move countと書かれている)を持たせると、「policyの正解率が23.8%、vlaueの正解率が64.8%に改善した」という記事を書かれています。
AlphaZero方式における入力の正規化
http://tadaoyamaoka.hatenablog.com/entry/2019/02/27/002239
そこで、NNUEでもgamePlyを入力の特徴量として与えれば強くなるのではないかと思うのですが、よく考えてみると、NNUEのように駒の位置を入力特徴量にしていて、そのあとが全結合の場合、ニューロン1個で表現できるのです。
具体的に言いますと、例えば、76に先手の歩がある局面。これは初期局面から(少なくとも)1手要します。歩は後退できないので、歩の位置によって、初期局面から何手要したかがわかります。同様に他の駒もバックしない限りは何手要したかがわかります。
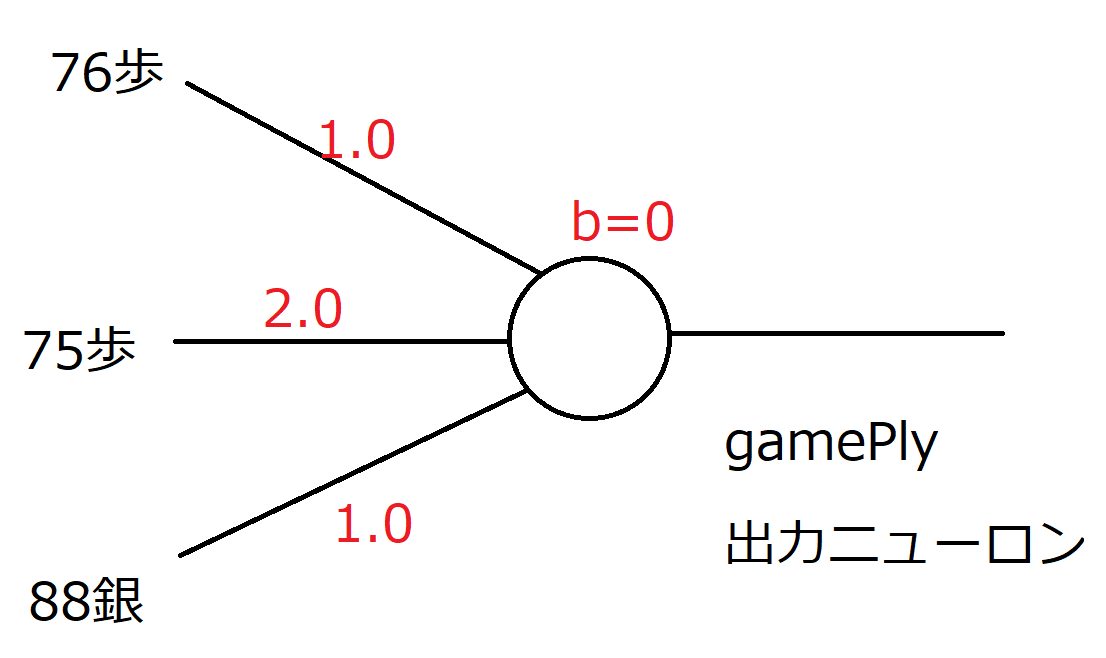
駒がバックしたときや手駒になったときに何手用したかは怪しいですが、少なくとも序盤か中終盤かの判定ぐらいには使えそうです。従来の将棋ソフトでは、『技巧』などが進行度というパラメーターを持っていましたが、その進行度に相当するものが1つのニューロンで表現できる(or すでに出来ている)と言えそうです。
そんなわけでNNUE型の入力の特徴量としてgamePlyを追加してやる試みは徒労に終わりそうです。
次回記事に続く。
