【連載】評価関数を作ってみよう！その5

前回の続き。

今回は1つの升に複数の利きがある時にどれだけ価値が減るのかということについて考えていきます。

これって機械学習なの？

この連載、勝率を最大化するパラメーターを求めるために3000局～数万局の対局をさせているのですが、この行為自体が一種の機械学習なのではないかという指摘がありました。

もしそうだとしたら、自己対局をして勝率の高いほうを採用するのも機械学習であることになってしまうと思うのですが。

まあ、その判断は読者に委ねますが、この連載に出てくるパラメーターの数は極めて少ないので手でも調整可能な範囲ですし、これを機械学習と呼ぶ人はあまりいないように思います。

同じ升に複数の利きがある時の価値

同じ升に利きが5つあるからと言って利きの価値が、利きが1つの時の5倍にはならないことは自明でしょう。相手の玉を捕まえようと考えた場合、一箇所に集中しているよりは点在しているほうが(包囲網的には)嬉しいはずです。

そう考えると、一つの升に複数の利きがある時にその価値は何らか減少していくはずです。

ある升にn個の利きがある時の価値 = n　×　その升に利きが1つの時の価値 ×　何らかの減少する関数

となるはずです。

こう考えた時、少なくとも、n個の利きよりはn+1個の利きのほうが良い状態ではあるので、後者のほうが価値は高くならないとおかしく、「何らかの減少する関数」は、その条件をクリアする必要があります。

そう考えると、pow(0.9 , n-1)のような関数を持ってきてしまうと、ある升の利きの数n( n ≧ 1 )に対して、その升の利きの価値は

　　利きが1個ある時の価値 × pow(0.9,n-1) × n

となり、これは n→∞ で 0に収束してしまうので、「なんか違うんじゃね？」となります。

// 1つの升に利きをつけられる最大は、8近傍 + 桂2箇所から = 10個ですから、 n ≦ 10 の範囲で単調に減少していなければ、まあ問題ないのですが。

n→∞で一定値に収束するほうが納得感があるので、

c1,c2を定数として、
ある升にn個の利きがある時の価値 = c1 – c2 * pow(X,n-1)
// n→∞でc1に収束する。また、n = 1のときに 1.0 になるものとする。

みたいな式になっていて欲しいですね。

1升に複数の利きがある時にどのように減衰するのかoptimizerに聞いてみた

そこである升の利きの数が n のときにどれだけの価値があるのかをoptimizerに尋ねてみました。n = 0のときは0で、n = 1のときは1024(== 1.0)は固定してあるものとします。

// optimizerの答え
int multi_effect_value&#91;11] = { 0 , 1024 , 1800 , 2300 , 2900 , 3500 , 3900 , 4300 , 4650 , 5000 , 5300 }

1 2	// optimizerの答え int multi_effect_value[11] = { 0 , 1024 , 1800 , 2300 , 2900 , 3500 , 3900 , 4300 , 4650 , 5000 , 5300 }

あまり細かい値までとるのは大変だったので100単位の数字となっていますが、だいたいの特徴はわかります。

また、これは、例えば5300という数値は、1升に利きが10個あるときに5300(利きが1つのときの 5300/1024 倍の価値がある)と設定した時に勝率が最大化されたという意味ではあるのですが、そもそも1升に10個も利きがあることなんて実戦でまずありえないので、このへんは計測自体が不正確です。

実戦で出現しないので、この値に設定して勝ったからと言って、その探索時に利きが1升に10個ある状態が一度も出現していないのであれば、その対局の結果はノイズでしかないからです。

そんなわけでして、いかにoptimizerと言えども実戦で出現しにくい形に関しては正確な答えを教えてくれないのです。今回のケースで言うと利きが4個以上の場合ですとあまり正確ではないはずです。

ともかく、optimizerの答えは、(実際は違うのかも知れませんが)指数関数的な減衰っぽい感じに見えます。

定数をうまく決定して、二乗誤差が最小になるようにしましょう。これには、Excelのゴールシーク機能を活用するのがお手軽です。

まず、Excelのゴールシークを使って二乗誤差が最小化するようにしました。そのあと、より正確な値をoptimizerを用いて調整した結果、以下式のようになりました。

利きがm個(m≧1)ある時の価値 = 6365 – pow(0.8525,m-1)*5341
// 値は1024倍されているので1024で割る必要があります。

この式は、利きがある升に無限個あったとしても、その価値は、利きが1つの時の6365/1024 = 6倍ちょいぐらいの価値しかないよと言っています。

本当にそうなのかわかりませんけど、八方桂とか特殊な駒を導入して、この最大値がどれくらいになるのか検証してみると面白いかもしれませんね。

今回のソースコード

// 王様からの距離に応じたある升の利きの価値。
int our_effect_value  &#91;9];
int their_effect_value&#91;9];

// 利きが一つの升に複数あるときの価値
// optimizerの答えは、{ 0 , 1024/* == 1.0 */ , 1800, 2300 , 2900,3500,3900,4300,4650,5000,5300 }
//   6365 - pow(0.8525,m-1)*5341 　みたいな感じ？
int multi_effect_value&#91;11];

void init() {

    for (int d = 0; d &lt; 9; ++d)
    {
        // 利きには、王様からの距離に反比例する価値がある。
        our_effect_value&#91;d]   = 85 * 1024 / (d + 1);
        their_effect_value&#91;d] = 98 * 1024 / (d + 1);
    }

    // 利きがm個ある時に、our_effect_value(their_effect_value)の価値は何倍されるのか？
    // 利きは最大で10個のことがある。
    for (int m = 0; m &lt; 11; ++m)
        multi_effect_value&#91;m] = m == 0 ? 0 : int(6365 - std::pow(0.8525, m - 1) * 5341);
}

Value compute_eval(const Position&amp; pos) {
    auto score = pos.state()->materialValue;

    for (auto sq : SQ)
    {
        // この升の先手の利きの数、後手の利きの数
        int effects&#91;2] = { pos.board_effect&#91;BLACK].effect(sq) , pos.board_effect&#91;WHITE].effect(sq) };

        // 盤上の升の利きの価値
        for (auto color : COLOR)
        {
            // color側の玉に対して
            auto king_sq = pos.king_square(color);

            // 筋と段でたくさん離れているほうの数をその距離とする。
            int d = dist(sq, king_sq);

            int s1 = multi_effect_value&#91;effects&#91; color]] * our_effect_value  &#91;d] / (1024 * 1024);
            int s2 = multi_effect_value&#91;effects&#91;~color]] * their_effect_value&#91;d] / (1024 * 1024);

            // scoreは先手から見たスコアなので、colorが先手の時は、(s1-s2) をscoreに加算。colorが後手の時は、(s2-s1) を加算。
            score += color == BLACK ? (s1 - s2) : (s2 - s1);
        }

        auto pc = pos.piece_on(sq);
        if (pc == NO_PIECE)
            continue;

        // 盤上の駒に対しては、その価値を1/10ほど減ずる。
        auto piece_value = PieceValue&#91;pc];
        score -= piece_value * 104 / 1024;
    }

    return pos.side_to_move() == BLACK ? score : -score;
}

// 王様からの距離に応じたある升の利きの価値。

int our_effect_value [9];

int their_effect_value[9];

// 利きが一つの升に複数あるときの価値

// optimizerの答えは、{ 0 , 1024/* == 1.0 */ , 1800, 2300 , 2900,3500,3900,4300,4650,5000,5300 }

// 6365 - pow(0.8525,m-1)*5341 　みたいな感じ？

int multi_effect_value[11];

void init() {

for (int d = 0; d < 9; ++d)

{

// 利きには、王様からの距離に反比例する価値がある。

our_effect_value[d] = 85 * 1024 / (d + 1);

their_effect_value[d] = 98 * 1024 / (d + 1);

}

// 利きがm個ある時に、our_effect_value(their_effect_value)の価値は何倍されるのか？

// 利きは最大で10個のことがある。

for (int m = 0; m < 11; ++m)

multi_effect_value[m] = m == 0 ? 0 : int(6365 - std::pow(0.8525, m - 1) * 5341);

}

Value compute_eval(const Position& pos) {

auto score = pos.state()->materialValue;

for (auto sq : SQ)

{

// この升の先手の利きの数、後手の利きの数

int effects[2] = { pos.board_effect[BLACK].effect(sq) , pos.board_effect[WHITE].effect(sq) };

// 盤上の升の利きの価値

for (auto color : COLOR)

{

// color側の玉に対して

auto king_sq = pos.king_square(color);

// 筋と段でたくさん離れているほうの数をその距離とする。

int d = dist(sq, king_sq);

int s1 = multi_effect_value[effects[ color]] * our_effect_value [d] / (1024 * 1024);

int s2 = multi_effect_value[effects[~color]] * their_effect_value[d] / (1024 * 1024);

// scoreは先手から見たスコアなので、colorが先手の時は、(s1-s2) をscoreに加算。colorが後手の時は、(s2-s1) を加算。

score += color == BLACK ? (s1 - s2) : (s2 - s1);

}

auto pc = pos.piece_on(sq);

if (pc == NO_PIECE)

continue;

// 盤上の駒に対しては、その価値を1/10ほど減ずる。

auto piece_value = PieceValue[pc];

score -= piece_value * 104 / 1024;

}

return pos.side_to_move() == BLACK ? score : -score;

}

今回の改良でどれだけ強くなったの？

今回の改良で前回から +R40 程度強くなりました。
Ryzen Threadripper 3990XでR2550～2650程度でしょうか。(もう少し強いかも)

奨励会レベルを突破するのはもう少し先になりそうです。

だからKPPT型は間違っている

ここまでの実験により、1つのマスに、味方の利きがn個(複数)ある時、その価値はn倍よりは減少することがわかりました。(相手の利きについても同様)

これをKPPT型の評価関数(玉とそれ以外の２駒からなる３駒関係)では、この減少をうまく捉えられるのでしょうか？

まず、遠方駒(飛・角・香)に関してはKPPT型ではその升まで利きが到達しているかどうかがわかりませんので、遠方駒に関しては利きの評価自体がおかしいことになります。

例えば、88の角の利きに関してであれば、実戦において88に角がいるときに、その利きが平均的にはどこまで到達しているかを考えて、その利きの価値を均した値が「88の角」の価値(位置評価)に上乗せされていると考えられます。

近接駒(遠方駒以外)の場合であれば、2つの利きがある升にある時にその価値を減少させること自体はできていると考えられます。

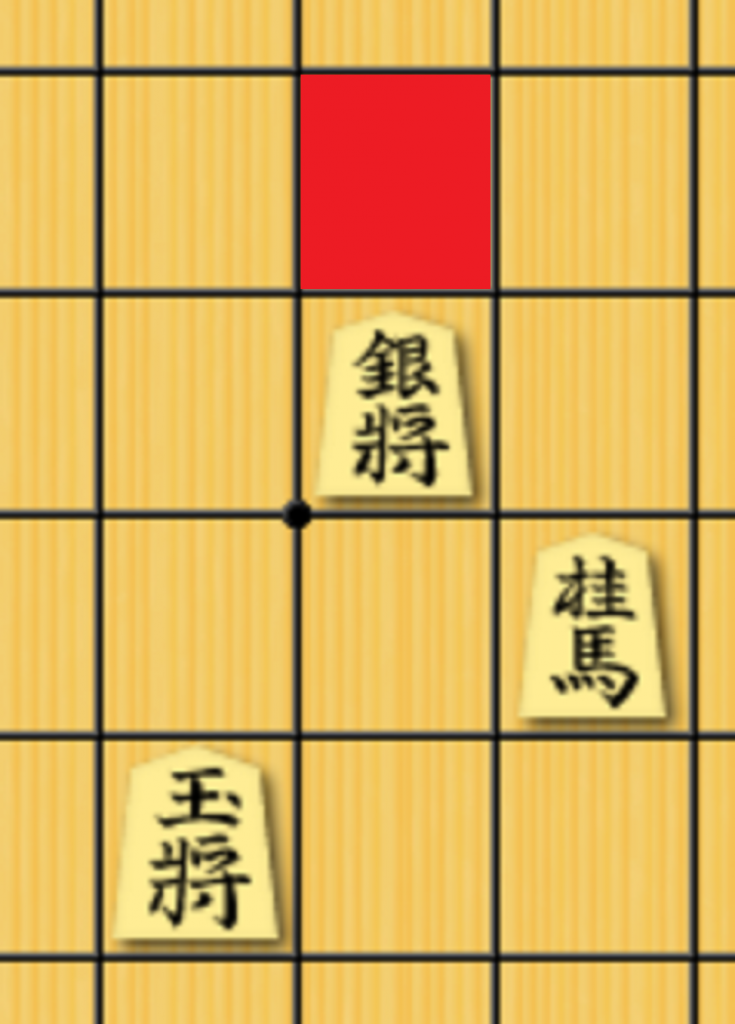
例えば上の赤い升には銀と桂の両方の利きがあり、この升の味方の利きは2個ですが、2個なので、利きが1つの時の価値の2倍ではなく、1.8倍程度になっているものと思われます。

// さきほどのoptimizerからの答えによると、2個の時は1.8倍(1800/1024)、3個の時は2.3倍(2300/1024)だったので。

ところが、ある升に3つ以上の利きがある場合はどうでしょうか？

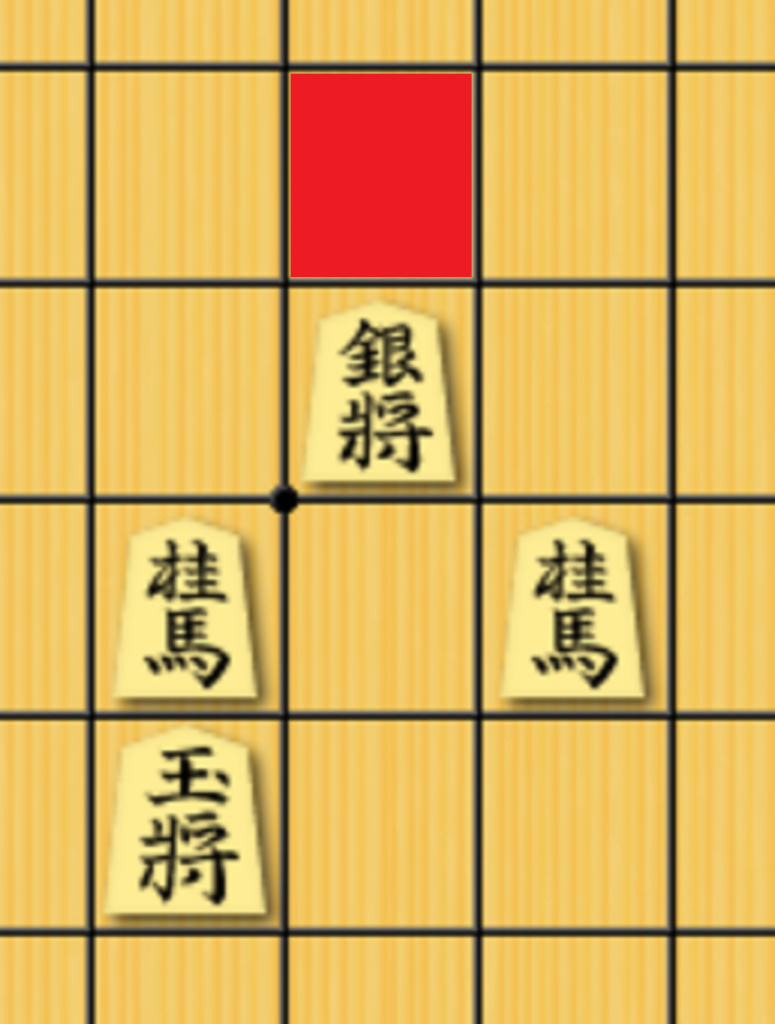
上の赤い升には、銀と2枚の桂が利いています。KPPT型ですと、このとき、
・玉-左の桂-銀
・玉-右の桂-銀
・玉-左の桂-右の桂
という3通りの関係について点数を加算します。

すると、この時、赤い升の利きの価値に関しては、1.8(2個利いているので)×3通り = 5.4個分の利きの価値であると計算されてしまいます。

これは加算しすぎになっていると考えられます。(実戦である升に2つの利きがある局面のほうが、ある升に3つの利きがある局面より圧倒的に多いため、2つの利きがある局面のほうに重きがおかれているはず。)

まあ、実戦で1つの升に3つの利きがある局面自体があまり出てきませんから、これによりどれだけ弱くなっているのかというと、微妙なところです。ここを正確に計算するコストと(計算時間)が、それによって強くなる分に見合うかどうかはわかりません。

ただ、このように駒や利きが密集した時に過大評価されてしまうのはKPPT型の弱点であると言えそうです。

これまで見てきたように利きから考えることで、「利きの価値はこう計算されているべき！」と既存の評価関数に駄目出しをすることはできるのですが、そこを正確にすることによって既存の評価関数より強い評価関数が作れるかどうかは別の問題です。出現頻度の低い局面で多少評価値にノイズがあっても、それは全体としては無視できるでしょうし。

まあ、だとしても、こうして利きの価値がどれだけあるのかを知っていると、良い評価関数を設計する指針にはなりそうです。

次回予告

次回「入玉した王様、なんで寄せにくいのん？」です。お楽しみに。(予告とは、異なる内容の場合がございます。予めご了承願います。)

つづく