前回の続き。今回は入玉模様の将棋について考えます。

これで玉、囲います？

味方の利きの価値は玉からの遠さに反比例するので、味方の利きの多いところに玉を移動させるような指し手はときどきあります。

あるいは敵の利きの集中しているところからは逃れたほうが得なので、敵の勢力から逃れるための玉移動もあります。

そんなわけで、利きによる磁場みたいなものが出来ていて、(利きに関して)得なほうに玉を移動していきます。

また玉のまわりに利きがあるほうが得なので玉の周りに駒を移動させようとします。

しかし、それを囲いと呼ぶにはあまりにも原始的なので、まだ囲いを作るためには欠けている評価因子がたくさんあるということですね。その評価因子が何なのかについては、後々考えていきましょう。

前回記事で、守りの利きと攻めの利きの価値の係数が以前と変わってるんですけど？

利きには、王様からの距離に反比例する価値があることは、この連載の第二回でやりました。

85と98がその重みです。第二回でやった時は、この値が68と96でした。前回記事では85と98でした。調整している時にここの値が変えました。(変わりました) このように何かを追加して、最適な値が変わることはよくあります。

例えば、連載第一回目で、盤上の駒の価値は手駒に比べて104/1024だけ価値が低いというのをやりましたが、盤上の利きは盤上の駒によって発生するものなので、盤上の利きをプラス評価した場合、それは間接的に盤上の駒の価値に上乗せしていることになります。

つまり、利きの評価とは、盤上の駒のpositionalな(位置の)評価の一つの側面なのです。いままで、positionalな駒の価値について何も考えてきませんでしたが、利き自体が盤上の駒によって発生しうるものなので、positionalな評価を間接的にしていることになります。

そう考えると、利きの評価を行うと間接的に盤上の駒の効果が向上するので、盤上の駒の価値が(均した時に)手駒の価値の104/1024だけ低いというのなら、そうなるように、盤上の駒の価値を以前計算した時の価値より下げないといけない――というように、新しい評価項目を導入すると以前の値がバランスを保つために変わることはありえます。

この連載では、新しく評価項目を追加した時に、こうやって、パラメーターを調整することがあるので連載が進むにつれて値が変わっていることがあります。それは、上のような理由ですので、予めご了承ください。

守りの利きと攻めの利きの価値は何故違うのですか？

さきほどの利きの価値の係数は、85と98でした。

つまり、自玉から見た、守りの利き(自駒による利き)と攻めの利き(相手の駒による利き)とでは、後者のほうが価値が高いということです。何故ここが非対称なのでしょうか？

将棋は攻める側が有利(?)なゲームだと言うのは、将棋指しなら感覚的には理解していて、例えば次の局面はどうでしょうか。

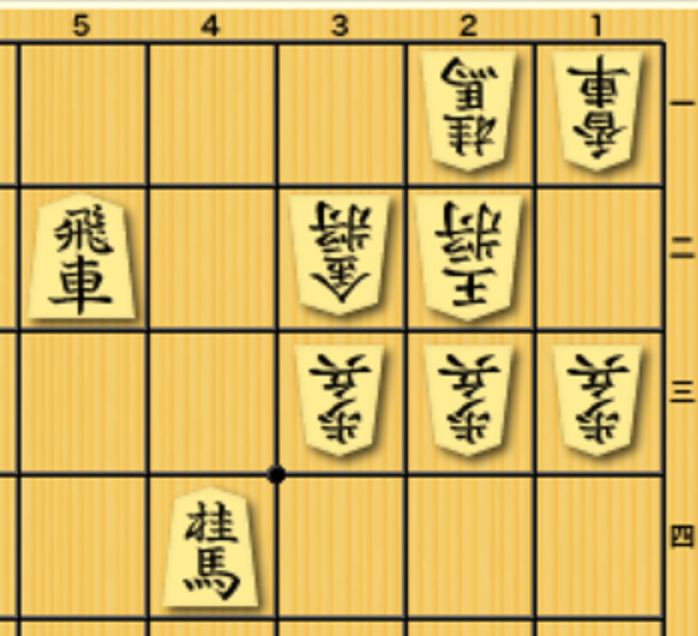
先手は桂で金を取れそうですが、後手はこの金を守るのが容易ではないです。仮に桂を持っていたとしても、32の金に利かすように打てません。先手は何度でも桂を44から打って32の駒を剥がせるのに、です。

これは、32の升に下から桂を利かせることができないため(盤の外になってしまう)で、桂という駒の動きが上下に対して非対称であることから生じる問題です。チェスの場合ですと、その駒の動きはPawn(将棋で言う歩)以外は、上下対称なので事情が少し違ってくるのかも知れませんね。

入玉下手すぎるんですけど？

前回の評価関数でR2600ぐらいですが、このレベル帯の将棋であっても、5%ぐらいは入玉模様の将棋になります。(もっと強いプレイヤーですと、入玉模様の将棋はもっと増えます)

しかしいまの状態ですと、するすると相手の王様を上部に逃がしてしまいます。これは何故かと言うと、自陣にやってきた相手の王様を攻めにくいというのをこの評価関数は知らないからです。

そもそもで言うと、入玉された時に何故攻めにくいのでしょうか？

これも将棋指しならば誰でも知っていると思いますが、王手自体がかける駒が制限されるのです。

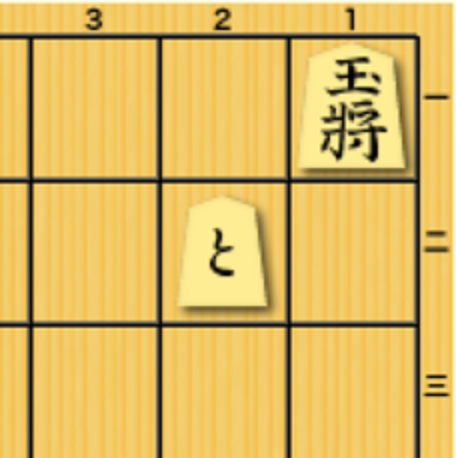
上図の王様を後手が王手しようと思うと、「歩」「香」「桂」では王手自体がかかりません。王手がかからないことには詰ませることは不可能なので、これらの駒だけが千枚あっても詰みません。まあ、こう書くと将棋指しからは「歩が千枚あったら、成駒にして引いていけば詰むよ」とか「歩が30枚あれば宣言勝ちすればいいっしょ」とか色々コメントいただくんですけどね。😅

ともかく上図、王様以外の7種類の駒のうち3種の駒が無力化されています。おまけに、銀・角での王手も直接はかかりません。(22の「と」を払わない限りは。)　そう考えると、5/7種類の駒が無力化されているわけです。

このような詰ませにくさは、将棋の駒が前には利くけども後ろには利かないという上下(前後？)の非対称性からくるものです。つまり、さきほどの「守りの利きと攻めの利きの価値が異なる」という問題と同じところに根ざしている問題です。

駒の動きが完全に上下対称であれば、この問題は起きないのかと言うと、あまりそうとも言えなくて、promotion(成り)の問題があります。歩を成って「と」にして、それで攻めるとか、入玉した自玉を守るとか、そういうことができてしまうので、そういう意味では、王様のいる升によって攻めやすさが異なるのはある意味必然です。

しかし、今回の評価関数は利きしか見ていないので、このような王様のいる升の違いによる攻めやすさ/攻められやすさの違いをうまく捉えられていません。

それが入玉が下手な原因なのですが、これを玉のpositionalな評価なしに回避するのはわりと難しいです。

結論だけ書いておきますと、1段目にいる先手玉に+2100点、2段目なら1000点、3段目なら600点を加点すると、+R10ぐらい強くなります。(いずれも歩の価値を90点とするときの点数)　また、99の升にいる玉(穴熊だと思われる)に+100点を加点すると+R5ぐらい強くなります。これらはoptimizerによって得られた値です。以前も書きましたが、実戦であまり出現しない形に関しては値の精度はそんなになくて、入玉将棋もこれに該当します。なので、2100点という数字にはわりと誤差があると考えてください。

// 他の特徴量を追加していくと、この値は徐々に下がっていきます。

まあ、1段目にいる玉に、2100点の価値ありということは、歩に換算すると、2100/90 ≒23.3なので、約20枚分の歩の価値(10枚の歩得)があるということですね。第一回に駒の価値のテーブルが書いてあって、そこを見ると飛車の価値が990ですので、1段目への入玉は飛車得(990×2)と同じ価値があるということですね。これは将棋指しの皆様の感覚に合致しているでしょうか？

こうして、「1段目への入玉は飛車得に相当する」って、新しい将棋の格言が誕生しました。😉

いずれにせよ、このように盤上には寄せやすい升と寄せにくい升が存在している以上、それを玉のpositionalな価値として足してやると強くなるというのは当然のことなのです。

入玉加点の歴史

Bonanzaのソースコードが公開された当時(2009年)、機械学習を導入した当時、プロの棋譜を機械学習に用いていたので、入玉模様の将棋の棋譜が圧倒的に足りていなくて、Bonanzaでは入玉模様の将棋が苦手だと言われていました。

第二回電王トーナメント(2014年)のころも、Bonanzaを改造して出てきているチームにはこの問題があって、開発者は、こっそり、入玉加点として上のような加点をしていました。(敵陣のそれぞれの升に対してこれをうまく調整してやると+R20ぐらいあがる) その少しあとになって公開されたAperyのソースコードにも入玉用の加点テーブルが存在していました。

このように、将棋ソフトで自ら自己対局で教師を作りそこから学習させる強化学習をはじめるまでは、入玉加点が普通に行われていました。

そんなわけでして、今回の連載ではなるべく直接的なpositionalな評価は導入しないようにしているものの(positionalな価値の正体が何であるのかを突き止めたいため)、入玉に関しては将棋の駒の特性に依るところが大きいので、この部分をうまくモデル化することは難しいと私は考えていて、それなら入玉に関しては加点するコードを書くのも仕方ないかなと思っています。

次回予告

次回「大きなテーブル使っていいなら、これめっちゃ速くなるんですけど？」です。お楽しみに。(予告とは、異なる内容の場合がございます。予めご了承願います。)

つづく